الگوریتم پریم Prim’s Algorithm

الگوریتم پریم Prim’s Algorithm

الگوریتم پریم Prim’s Algorithm یک الگوریتم حریصانه برای یافتن درخت پوشای کمینه MST است. الگوریتم پریم، الگوریتمی در نظریه گراف‌ها است که درخت پوشای مینیمم را برای یک گراف همبند وزن دار ( همبندی یعنی حداقل تعداد رأس‌ها یا یال‌هایی است که با حذفشان، ارتباط رأس‌های باقی‌مانده از بین نرود) پیدا می‌کند. یعنی زیرمجموعه‌ای از یال‌ها را در آن گراف می‌یابد که درختی را تشکیل می‌دهند که همه راس ها را شامل شود و دارای حداقل هزینه یال ها باشد.

مقدمه

این الگوریتم در سال ۱۹۳۰ توسط ریاضیدانی به نام جارنیک داده شد و سپس در سال ۱۹۵۷ پریم، دانشمند علوم کامپیوتر آن را مستقل از جارنیک کشف کرد و در سال ۱۹۵۹ دایکسترا دوباره به آن دست یافت. از این رو این الگوریتم گاهی با نام الگوریتم DJP نیز شناخته می‌شود که برگرفته از اسامی دایکسترا، جارنیک و پریم است. از این نوع دسته الگوریتم ها می توان به الگوریتم کروسکال و سولین نیز اشاره کرد.

ایده اصلی الگوریتم پریم این است که دو مجموعه ای از رأس ها را نگه می دارد. مجموعه اول شامل رأس هایی است که قبلا در MST موجود است، مجموعه دیگری حاوی رأس هایی است که هنوز موجود نیستند. در هر مرحله همه لبه هایی که دو مجموعه را متصل می کنند را بررسی می کند و لبه ها با حداقل وزن انتخاب می شوند. پس از برداشتن لبه، نقطه انتهایی دیگر لبه را به مجموعه حاوی MST منتقل می کند.

الگوریتم Prim چگونه کار می کند؟

ایده پشت الگوریتم Prim، ساده است، درخت پوشا به این معنی است که تمام رأس ها باید متصل شوند. بنابراین دو زیرمجموعه از رأس ها باید متصل شوند تا یک درخت پوشا ایجاد شود. و آنها باید با حداقل لبه وزن ارتباط داشته باشند تا درخت پوشا کمینه ایجاد شود. شبه کد الگوریتم پریم بصورت زیر است.

1) Create a set mstSet that keeps track of vertices already included in MST.
2) Assign a key value to all vertices in the input graph. Initialize all key values as INFINITE. Assign key value as 0 for the first vertex so that it is picked first.
3) While mstSet doesn’t include all vertices
….a) Pick a vertex u which is not there in mstSet and has minimum key value.
….b) Include u to mstSet.
….c) Update key value of all adjacent vertices of u. To update the key values, iterate

تعیین درخت پوشای مینیمم با الگوریتم پریم در پایتون

این سورس کد به زبان پایتون نوشته شده و درخت پوشای مینیمم را با استفاده از الگوریتم پریم حل می‌کند. برای دانلود سورس کد بر روی لینک زیر کلیک نمایید.

همین الان کلیک کنید

مثال الگوریتم پریم

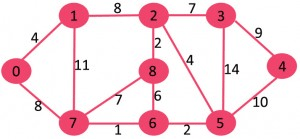
برای درک بهتر الگوریتم گراف زیر را در نظر می گیریم. این گراف یک گراف همبند وزن دار بدون جهت است.

مجموعه mstSet در ابتدا خالی است و کلید های اختصاص داده شده به رأس ها عبارتند از {0، INF، INF، INF، INF، INF، INF، INF} که INF نشان دهنده بی نهایت است. ابتدا رأس با حداقل مقدار کلیدی انتخاب می شود. بنابراین {mstSet {0 می شود. پس از وارد شدن به mstSet، مقادیر کلیدی رأس های مجاور را به روز رسانی کنید. رأس های مجاور 0 راس های 1 و 7 هستند. وزن راس های 1 و 7 به ترتیب 4 و 8 به روز می شوند. پس از زیرگراف ردیف ها و مقادیر کلیدی آنها را نشان می دهد، تنها رأس ها با مقادیر کلید محدود نمایش داده می شوند. راس های موجود در MST در رنگ سبز نشان داده شده است.

رأس با حداقل مقدار کلیدی را انتخاب کنید که در MST (نه در mstSET) موجود نیست. رأس 1 برداشته شده و به mstSet اضافه می شود. بنابراین mstSet اکنون {0، 1} می شود. مقدار کلیدی رأس های مجاور 1 را به روز رسانی کنید. مقدار کلیدی رأس 2 به 8 می رسد.

دوباره رأس با حداقل مقدار کلیدی را انتخاب کنید که در MST (نه در mstSET) موجود نیست. ما می توانیم راس 7 یا راس 2 را انتخاب کنیم، راس 7 را انتخاب کنیم. بنابراین mstSet اکنون {0، 1، 7} می شود. ارزش کلیدی رأس های مجاور 7 را به روز رسانی کنید. مقدار کلیدی رأس 6 و 8 به ترتیب محدود می شود (1 و 7 به ترتیب).

باز رأس با حداقل مقدار کلیدی را انتخاب کنید که در MST موجود نیست. راس 6 برداشته می شود. بنابراین mstSet اکنون {0، 1، 7، 6} می شود. ارزش کلیدی رأس های مجاور 6 را به روز کنید. ارزش کلیدی رأس 5 و 8 به روز می شود.

گام های فوق را تکرار کنید تا mstSet شامل تمام رأس های گراف داده شده باشد. در نهایت، ما نمودار زیر را بدست می آوریم.