الگوریتم کروسکال Kruskal’s algorithm

الگوریتم کروسکال Kruskal’s algorithm یک الگوریتم حریصانه (Heuristic) برای یافتن درخت پوشای کمینه MST است. الگوریتم کروسکال، الگوریتمی در نظریه گرافها است که درخت پوشای مینیمم را برای یک گراف همبند وزن دار (همبندی یعنی حداقل تعداد رأسها یا یالهایی است که با حذفشان، ارتباط رأسهای باقیمانده از بین نرود) پیدا میکند. یعنی زیرمجموعهای از یالها را در آن گراف مییابد که درختی را تشکیل میدهند که همه راس ها را شامل شود و دارای حداقل هزینه یال ها باشد.
مقدمه
همانطور که گفته شد با توجه به یک گراف متصل و همبند، درخت پوشا از آن گراف یک زیرگراف است که یک درخت است و تمام رأس ها را با یکدیگر متصل می کند. یک گراف تنها می تواند انواع درخت های مختلف را پوشش دهد. یک درخت پوشای کمینه (MST) یا درخت پوشای مینیمم درختی برای یک گراف وزن دار، متصل یک درخت پوشا با وزن کمتر یا برابر با وزن هر درخت دیگر است. وزن یک درخت، مجموع وزن های داده شده به هر لبه درخت است.
درخت پوشای کمینه Minimum Spanning Tree
درخت يک گراف متصل بدون حلقه است. يک درخت پوشا (Spanning Tree) زيرگرافی از گراف G است که شامل کليه رئوس گراف G باشد و يک درخت باشد. بنابراين اگر گراف G دارای n گره باشد درخت پوشای آن دارای n-1 یال nhvn. پیمایشهای DFS و BFS هر کدام يک درخت پوشا تولید میكنند. تعداد درختهای پوشای یك گراف كامل با n گره برابر 2n-1-1 است.
درخت پوشای حداقل (Minimum Spanning Tree) گراف وزن دار G، درخت پوشائی است که مجموع وزن های آن حداقل باشد. برای بدست آوردن درخت پوشای حداقل الگوريتم کروسکال (Kruskal) و الگوريتم پريم (Prim) و الگوریتم سولین (Sollin) به روش حریصانه شروع به حل مسئله می کنند. دو الگوریتم پریم و کروسکال بطور کامل در همین سایت بررسی شده اند. در ادامه به بررسی و تشریح الگوريتم کروسکال خواهیم پرداخت.
الگوریتم کروسکال Kruskal’s algorithm
گراف G با n رأس را در نظر بگيريد. الگوريتم کروسکال به صورت زير عمل می کند:
1. تمام یال ها را به طور صعودی بر حسب وزن مرتب کنید.
2. درخت T را متشکل از گره های G بدون یال را ايجاد کنيد.
3. عملیات زیر را n-1 بارتکرار کنید:
4. یک یال با حداقل وزن را به درخت T اضافه کنید به طوری که حلقه ایجاد نشود.
گاهی چند يال دارای يک وزن هستند، در اين حالت ترتيب يال هایی که انتخاب می شوند مهم نيست. درخت های پوشای حداقل مختلفی ممکن است حاصل شود اما مجموع وزن آنها هميشه يکسان و حداقل می شود. پيچيدگی زمانی الگوريتم (O(mn می شود. که m تعداد يال ها و n تعداد رئوس گراف G است.
شبه کد الگوریتم کروسکال
Void kruskal (int n ,int m ,set _of_edges E,set_of_edges & F)
{
index i, j;
Set_pointer p , q ;
edge e;
Sort the m edges in E by weight in nondecreasing order ;
F=∅;
initial(n); //زیر مجموعه غیر الحاقی n مقدار دهی
While(number of edges in F is less than n-1){
e= edge with least weight not yet considered;
i, j = indices of vertices connected by e ;
p=find(i);
q=find(j);
if(!equal(p,q)){
merge(p,q);
add e to F ;
}
}
}
مثال الگوریتم کروسکال
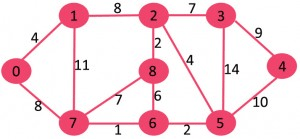
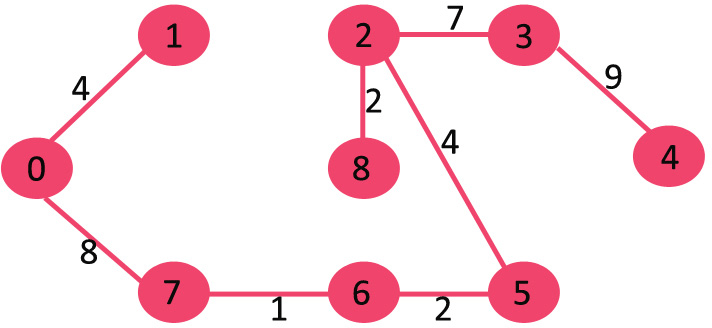
این الگوریتم یک الگوریتم حریصانه است پس انتخاب حریصانه انتخاب کوچکترین (کم هزینه ترین) وزن لبه است که باعث ایجاد چرخه ای در MST نشود. در مثال گراف ورودی را در نظر بگیرید.
این گراف شامل 9 رأس و 14 لبه است بنابراین، حداقل درخت پوشا تشکیل شده (9 – 1) = 8 لبه خواهد بود. ابتدا لبه ها را به ترتیب کوچکتر به بزرگتر یعنی صعودی مرتب می کنیم.
After sorting: Weight Src Dest 1 7 6 2 8 2 2 6 5 4 0 1 4 2 5 6 8 6 7 2 3 7 7 8 8 0 7 8 1 2 9 3 4 10 5 4 11 1 7 14 3 5
حالا همه لبه ها را یک به یک از فهرست لبه های مرتب شده انتخاب کنید.
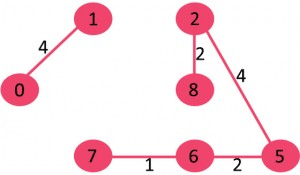
1- لبه 6-7 را انتخاب کنید: حلقه ای شکل نمی گیرد لبه به MST اضافه شود.
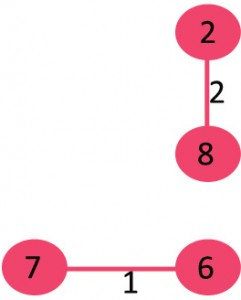
2- لبه 2-8 را انتخاب کنید: حلقه ای شکل نمی شود پس لبه به MST اضافه شود.
3- لبه 6-5 را انتخاب کنید: حلقه ای شکل نمی شود پس لبه به MST اضافه شود.
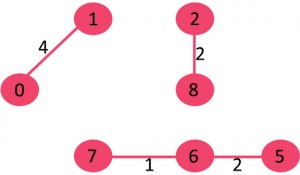
4- لبه 0-1 را انتخاب کنید: حلقه ای شکل نمی شود پس لبه به MST اضافه شود.
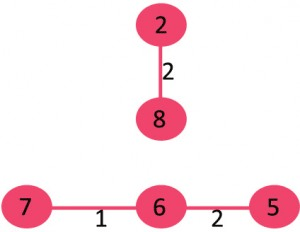
5- لبه 2-5 را انتخاب کنید: حلقه ای شکل نمی شود پس لبه به MST اضافه شود.
6- لبه 8-6 را انتخاب کنید: حلقه شکل می شود پس لبه به MST اضافه نمی شود.
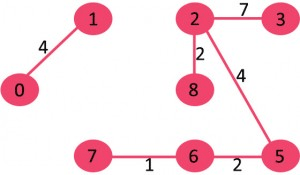
7- لبه 2-3 را انتخاب کنید: حلقه ای شکل نمی شود پس لبه به MST اضافه شود.
8- لبه 7-8 را انتخاب کنید: حلقه شکل می شود پس لبه به MST اضافه نمی شود.
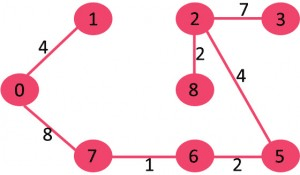
9- لبه 0-7 را انتخاب کنید: حلقه ای شکل نمی شود پس لبه به MST اضافه شود.
10- لبه 1-2 را انتخاب کنید: حلقه شکل می شود پس لبه به MST اضافه نمی شود.
11- لبه 3-4 را انتخاب کنید: حلقه ای شکل نمی شود پس لبه به MST اضافه شود.
از آنجا که تعداد لبه ها برابر است 8=(9-1)، الگوریتم در اینجا متوقف می شود.
سخن آخر
در پست الگوریتم کروسکال اطلاعاتی درباره این الگوریتم حریصانه که الگوریتمی در نظریه گرافها است و چگونگی استفاده از آن برای یافتن درخت پوشای کمینه MST خدمت شما عزیزان ارائه گردیده است. توضیحات درخت پوشای کمینه،الگوریتم کروسکال و شبه کدهای این الگوریتم به همراه شکل آنها از جمله موارد مهمی است که در این پست شرح داده شده اند.
- آموزش رسم فلوچارت — گام به گام همراه با مثال
- پیمایش درخت postorder در سی پلاس پلاس ++C
- الگوریتم جستجوی عرضی Breadth First Search — راهنمای جامع همراه با مثال
- پیمایش درخت postorder در سی پلاس پلاس ++C
- آموزش پیمایش درخت در ساختمان داده | جامع همراه با مثال
- سورس کد الگوریتم هافمن (Huffman) در سی پلاس پلاس ++C
- ساختمان داده و الگوریتم چیست – مبانی و اصطلاحات الگوریتم و ساختمان داده
- پاورپوینت الگوریتم بلمن فورد — یافتن کوتاه ترین مسیر
درباره امین جلیل زاده رزین
پایه گذار و موسس وب سایت آموزشی پی استور، مدرس دانشگاه فنی و حرفه ای، برنامه نویس و تحلیل گر سیستم، پژوهشگر در حوزه الگوریتم های ابتکاری، فرا ابتکاری، یادگیری ماشین، شبکه و پایگاه داده. ایشان در زبان های برنامه نویسی متعدد، نظیر ++C، سی شارپ، PHP ،Java، متلب MATLAB و Python تسلط و سابقه تدریس فعال دارند.
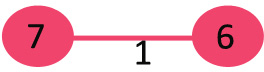





سورس الگوریتم پریم رو در پایتون میخوام
خدمت شما
سلام
مطمئن هستین که این فایل ها اجرا میشه چون میخوام بفرستم برا استادم و عجله دارم خواهشا جواب بدین
واینکه ویدئو محصول هم بالا نمیاد همش میزنه مشکلی رخ داده لطفا درستش کنید
سلام
بله تمامی محصولات تست شده وقابلیت اجرا دارند.
نطرات و دیدگاه های خود را با ما در میان بگذارید.