الگوریتم Sollin سولین تشریح همراه با مثال

الگوریتم Boruvka (الگوریتم Sollin)

الگوریتم Sollin یا همان الگوریتم Boruvka عنوان موضوعی است که در این پست به آن پرداخته می شود. ابتدا الگوریتم سولین تشریح می شود سپس مثال عملی از این الگوریتم زده می شود. برای اطلاهات بیشتر روی مفاهیم موجود در این پست به لینک هایی که گذاشته شده حتماً مراجعه کنید.

الگوریتم بروکا Boruvka چیست؟

الگوریتم Boruvka راهی برای پیدا کردن درخت پوشای کمینه است. یک درخت پوشای مینیمم درختی است که در آن مجموع وزن لبه به حداقل برسد. این اولین الگوریتمی بود که در سال 1926 برای پیدا کردن درخت پوشای کمینه MSTs طراحی شد.  آقای Otakar Boruvka از آن برای یافتن مسیریابی کارآمدترین شبکه برق استفاده کرده است. الگوریتم ها و روش های زیادی برای پیدا کردن درخت پوشای حداقل وجود دارد. الگوریتم Boruvka یک الگوریتم حریصانه است و مشابه الگوریتم Kruskal و الگوریتم Prim است. این روش اساساً حد وسط بین دو الگوریتم کروسکال و پریم است. این الگوریتم اغلب با نام الگوریتم Sollin نیز شناخته می شود. در کتاب های ساختمان داده اغلب از این روش با نام الگوریتم سولین یاد می شود.

تشریح الگوریتم Sollin

بر خلاف الگوریتم های پریم و راشال – کروسکال که در هر مرحله فقط یک یال به درخت اضافه می کردند در الگوریتم سولین چندین لبه را برای درخت اضافه می کند. در ابتدا یک مرحله لبه های انتخاب شده، همراه با تمام n راس گراف، تشکیل یک درخت پوشا را می دهند. در خلال یک مرحله یک لبه برای هر درخت انتخاب می شود که دارای حداقل هزینه بوده یعنی اینکه دقیقاً دارای یک راس در درخت می باشد. از آنجا که دو درخت در جنگل می توانند یک لبه یکسان انتخاب کنند، لذا می توان کپی تکراری لبه ها را حذف کرد. در ابتدای مرحله اول مجموعه لبه های انتخاب شده خالی است. این الگوریتم هنگامی پایان می یابد که فقط یک درخت در انتهای یک مرحله باقی و یا هیچ لبه ای برای انتخاب باقی نمانده باشد. شبه کد الگوریتم Boruvka  به صورت زیر است:

1) Input is a connected, weighted and directed graph.
2) Initialize all vertices as individual components (or sets).
3) Initialize MST as empty.
4) While there are more than one components, do following
   for each component.
      a)  Find the closest weight edge that connects this 
          component to any other component.
      b)  Add this closest edge to MST if not already added.  
5) Return MST.

سورس کد تعیین درخت پوشای کمینه با الگوریتم sollin در پایتون

این سورس کد به زبان پایتون نوشته شده و درخت پوشای کمینه را با استفاده از الگوریتم سولین حل می‌کند. برای دانلود سورس کد بر روی لینک زیر کلیک نمایید.

همین الان کلیک کنید

مثال الگوریتم سولین (Sollin)

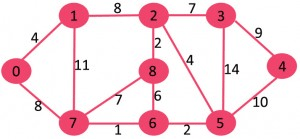
برای مثال گراف شکل زیر را همراه با هزینه هر لبه در نظر می گیریم.

ابتدا MST یا درخت پوشا خالی است هر رأس یک جزء یا مولفه تنها  است که در زیر نمودار با رنگ آبی مشخص شده است.

برای هر جزء، ارزان ترین لبه را پیدا کنید که آن را به یک جزء دیگر متصل می کند.

Component                Cheapest Edge that connects 
                         it to some other component
  {0}                           0-1
  {1}                           0-1
  {2}                           2-8
  {3}                           2-3
  {4}                           3-4
  {5}                           5-6
  {6}                           6-7
  {7}                           6-7
  {8}                           2-8

ارزان ترین لبه با رنگ سبز مشخص شده است. اکنون MST 0-1، 2-8، 2-3، 3-4، 5-6، 6-7 می شود.

بعد از مرحله بالا اجزاء یا همان زیر دختان {{0،1}، {2،3،4،8}، {5،6،7}} می باشد. اجزاء با رنگ آبی محاصره می شوند.

در مرحله بعد دوباره گام قبلی را برای مشخص کردن ارزان ترین لبه تکرار می کنیم، به عنوان مثال، برای هر جزء، ارزان ترین لبه را پیدا می کنیم که آن را به برخی اجزای دیگر متصل می کند ( یعنی به درختان دیگر متصل کند نه اعضای جزء خودش)

Component                Cheapest Edge that connects 
                         it to some other component
  {0,1}                        1-2 (or 0-7)
  {2,3,4,8}                    2-5
  {5,6,7}                      2-5

در مرحله آخر تنها یک جزء {0، 1، 2، 3، 4، 5، 6، 7، 8} وجود دارد که همه لبه ها دارد. از آنجا که تنها یک جزء وجود دارد، الگوریتم متوقف می شود و درخت ایجاد می شود. در نهایت درخت پوشا بصورت زیر خواهد بود و هزینه آن نیز برابر 37 خواهد بود.

الگوریتم سولین در سی پلاس پلاس (حل درخت پوشای کمینه با الگوریتم سولین)

سورس کد تعیین درخت پوشای کمینه با الگوریتم سولین در سی پلاس پلاس نوشته شده است. این برنامه مناسب برای دانشجویان و علاقه مندان به درس ساختمان داده و طراحی الگوریتم می باشد.

همین الان کلیک کنید