سورس کد الگوریتم جستجوی گرانشی GSA برای حل مسئله فروشنده دوره گرد TSP در متلب عنوان محصولی است که در این بخش ارائه شده است. حل مسئله فروشنده دوره گرد با الگوریتم های مختلف به عنوان چالشی برای بررسی قدرت آن الگوریتم و استفاده کاربردی از الگوریتم ارائه شده می باشد. در ادامه به توضیحاتی پیرامون مسئله خواهیم داشت.

برنامهنویس: تیم برنامه نویسی پی استور
متشکل از اساتید و فارغ التحصیلان رشته های فنی - مهندسی
تیم برنامه نویسی پی استور یکی از اولین گروه های تشکیل شده در مجموعه آموزشی پی استور می باشد. این تیم از اساتید مجرب و فارغ التحصیلان رشته های فنی و مهندسی تشکیل شده که در زمینه های مختلف برنامه نویسی و تهیه سورس کد فعال هستند.
الگوریتم جستجوی گرانشی GSA
الگوریتم جستجوی گرانشی gravitational search algorithm یا به اختصار GSA یک الگوریتم بهینه سازی جدید بر اساس قانون گرانشی است. این الگوریتم بر اساس قانون گرانش نیوتن است. هر ذره در جهان ذره دیگر را با نیرویی که رابطه مستقیم با ضرب جرم آنها و رابطه معکوس با مربع فاصله بین آنها دارد بهطرف خود جذب میکند.
در الگوریتم جستجوی گرانشی عامل ها بهعنوان ذرات و کارایی آنها بهعنوان جرمشان در نظر گرفته میشود. همه این ذرات همدیگر را با یک نیروی گرانشی جذب می نمایند و این نیروی گرانشی باعث میشود تا همه اشیاء یک حرکت کلی بهسوی اشیائی داشته باشند که جرمشان از اشیاء دیگر بیشتراست؛ بنابراین اشیاء از طریق یک ارتباط مستقیم که همان نیروی گرانشی است برای رسیدن به جواب های بهتر همکاری میکنند.
اشیاء سنگین که همان راه حل هایی بهتر هستند آهسته تر از بقیه اشیاء حرکت میکنند و این حرکت آهسته می تواند مرحله بهره برداری را برای الگوریتم جستجوی گرانشی تضمین نماید.
در الگوریتم جستجوی گرانشی، هر جرم (عامل ) دارای چهار مشخصه زیر است:
- موقعیت
- جرم اینرسی
- جرم گرانشی فعال
- جرم گرانشی غیرفعال
موقعیت یک جرم مشخصکننده یک راه حل برای مسئله و جرم گرانشی و جرم اینرسی هر جرم مشخصکننده تابع برازش است بهعبارتیدیگر، هر جرم ارائهدهنده یک راه حل و الگوریتم با تنظیم جرم گرانشی و جرم اینرسی جستجوی فضای مسئله را ادامه می دهد. با گذشت زمان، ما انتظار داریم که جرم ها توسط جرم بزرگتر جذب شود این جرم نمایانگر یک راه حل بهینه در فضای جستجو است.
مسئله فروشنده دورگرد TSP
مساله فروشنده دوره گرد Travelling salesman problem یا به اختصار TSP مساله اي است که شرح آن خيلي آسان مي باشد. تعريف آن بدين صورت است که تعداد متناهي شهر با هزينه پيمايش بين هر جفت از آنها داده مي شود و هدف مساله اين است که يک فروشنده دوره گرد تمامي اين شهرها را به گونه اي ملاقات کند که هر يک از اين شهرها را فقط يک بارملاقات کرده و دوباره به شهر آغازين برگردد با اين شرط که با کمترين هزينه پيمايش اين کار را انجام دهد.
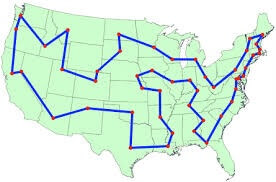
به طور کلي هدف پيدا کردن کم هزينه ترين تور براي ملاقات همه شهرها و بازگشت به شهر آغازين حرکت است. مساله فروشنده دوره گرد در شکل ساده و اختصاري با نام TSP شناخته مي شود. شکل زیر يک نمونه جواب از مساله فروشنده دوره گرد که در سال 1591 براي 15 شهر از کشور آمريکا مطرح شد را نشان مي دهد که با روش شاخه وحد حل شد.
سورس حل مسئله فروشنده دوره گرد TSP با الگوریتم GSA در متلب
در این قسمت سورس برنامه حل مسئله فروشنده دوره گرد TSP با الگوریتم جستجوی گرانشی GSA در متلب آماده شده است این سورس کد شامل 9 فایل می باشد که عبارتند از:
ویدئوی نحوه اجرا
درباره الگوریتم جستجوی گرانشی در متلب
سورس برنامه حل مسئله فروشنده دوره گرد TSP با الگوریتم جستجوی گرانشی GSA در متلب عنوان محصولی است که در این پست به آن پرداخته شده است. محصول در نرم افزار متلب نوشته شده و بصورت کامل توسط گروه پشتیبانی پی استور تست و اجرا شده است. محصول دارای نشان تضمین کیفیت پی استور می باشد. برای دانلود محصول آن را خریداری کنید.
مباحث مرتبط با حل مسئله فروشنده دوره گرد با الگوریتم های متاهیورستیک
مباحث مرتبط با الگوریتم جستجوی گرانشی GSA
الگوریتم جستجوی گرانشی GSA برای حل مسئله فروشنده دوره گرد TSP در متلب
| تاریخ انتشار: | 2 مرداد 1397 |
|---|---|
| تاریخ بروزرسانی: | 23 مهر 1397 |
| حجم فایل: | 3.8 کیلوبایت |
| فرمت فایل | m. در قالب متلب |
| مدت زمان: | 1.0 |
| شناسه اثر: | ندارد |
| هماهنگی با: | Matlab 2009 و بالاتر |
تاکنون 539 نفر این محصول را تهیه کرده اند و 1 نظر برای آن ثبت شده است.
نظرات و دیدگاه ها
قوانین ثبت دیدگاه
- لطفاً دیدگاه های خود را فارسی تایپ کنید.
- دیدگاه های نامرتبط به مطلب تایید نخواهد شد.
- از درج دیدگاه های تکراری پرهیز نمایید.
- سوالات تخصصی خودتان را از طریق تیکت پشتیبانی مطرح کنید.
الگوریتم جستجوی گرانشی GSA برای حل مسئله فروشنده دوره گرد TSP در متلب
هزینه سفارش: 139,000 تومان
| تاریخ انتشار: | 2 مرداد 1397 |
|---|---|
| تاریخ بروزرسانی: | 23 مهر 1397 |
| حجم فایل: | 3.8 کیلوبایت |
| فرمت فایل | m. در قالب متلب |
| مدت زمان: | 1.0 |
| شناسه اثر: | ندارد |
| هماهنگی با: | Matlab 2009 و بالاتر |
1 بازخورد (مشاهده نظرات)
هزینه سفارش: 139,000 تومان










مدیریت و پشتیبانی
نظرات و دیدگاه های خود را با ما درمیان بگذارید.