Name: تعیین درخت پوشای مینیمم با الگوریتم CMAES در متلب
Brand: پی استور
SKU: 5778
Price: 25000 IRT
Availability: instock
Rating: 5.00 (1 reviews)

تعیین درخت پوشای مینیمم با الگوریتم CMAES در متلب

در این پست به مسئله حل درخت پوشای مینیمم با الگوریتم CMAES در متلب پرداخته شده است. درخت پوشای مینیمم یا درخت پوشای کمینه درختی است از زیر مجموعه ای از گراف G که تمام رأس ها با حداقل تعداد ممکن لبه ها پوشیده شده است که دارای حداقل هزینه باشد. از این رو، در درخت پوشای مینیمم حلقه ای وجود ندارد و همچنین نمی تواند قطع باشد.

الگوریتم CMA-ES جزو الگوریتم های تکاملی یا فرا ابتکاری هستند که به یافتن پاسخ بهینه مسائل مختلف بهینه سازی می‌پردازد. این الگوریتم از یک توزیع نرمال، نمونه‌گیری کرده و جمعیت جدید را به وجود می‌آورد. این الگوریتم تکاملی یک ماتریس کواریانس و یک بردار میانگین را از جمعیت تخمین می‌زند. قوانین مختلف به روز‌رسانی، ماتریس کواریانس تطبیق یافته‌ای را در هر نسل ایجاد می‌کند که در کیفیت جمعیت جدید و در نتیجه هدایت تکامل نقش مهمی دارد.

درخت پوشای کمینه (مینیمم)

با توجه به یک گراف متصل و بدون جهت، درخت پوشا از آن گراف یک زیرگرافی است که اولاً یک درخت است و تمام رأس ها را با یکدیگر متصل می کند. یک گراف می تواند انواع درخت های مختلف را پوشش دهد. یک Minimum Spanning Tree درخت پوشای کمینه (MST) یا درخت پوشای مینیمال برای یک گراف وزنم دار، متصل و بدون جهت یک درخت پوشا با وزن کمتر یا برابر با وزن هر درخت دیگر است. وزن یک درخت، مجموع وزن های داده شده به هر لبه درخت است.

درخت پوشای کمینه

الگوریتم CMAES

این الگوریتم مخفف Covariance Matrix Adaptation Evolution Strategy به معنای استراتژی تکاملی انطباق ماتریس کوواریانس می باشد. دو اصل اصلی برای سازگاری پارامترهای توزیع جستجو در الگوریتم CMA-ES مورد استفاده قرار می گیرند.

ابتدا، یک اصل حداکثر احتمال maximum-likelihood، برای افزایش احتمال موفقیت راه حل های کاندید شده و مراحل جستجو در نظر گرفته می شود. متوسط توزیع به روز می شود به طوری که احتمال موفقیت پیشین موفق به راه حل های حداکثر می شود.

ماتریس کوواریانس توزیع (به طور تدریجی) به روز می شود به طوری که احتمال مراحل پیشین موفق جستجو افزایش می یابد. هر دو به روز رسانی را می توان به عنوان یک شیب طبیعی شناخت. همچنین، در نتیجه، CMA یک مولفه اصلی تکرار شده برای تجزیه و تحلیل مراحل جستجو موفق را در حالی که تمام محورهای اصلی را نگه می دارد انجام می دهد.

دوم، دو مسیر از زمان تکامل میانگین توزیع استراتژی ثبت شده، به نام مسیر جستجو یا تکامل می باشد. این مسیرها حاوی اطلاعات مهمی درباره همبستگی بین مراحل متوالی هستند.

به طور خاص، اگر مراحل متوالی در جهت مشابهی گرفته شود، مسیرهای تکاملی بلند می شوند. مسیرهای تکاملی از دو راه بهره برداری می شوند. یک راه برای روش انطباق ماتریس کوواریانس به جای مراحل موفقیت آمیز موفقیت آمیز استفاده می شود و باعث افزایش احتمال واریانس بسیار بیشتر جهت جهت مطلوب می شود. مسیر دیگر مورد استفاده برای کنترل اضافی اندازه گام است.

قسمتی از سورس محصول

clc;
clear;
close all;

%% Problem Definition

model=CreateModel();

CostFunction=@(xhat) CostFun(xhat,model);        % Cost Function

nVar=model.n*(model.n-1)/2;             % Number of Decision Variables

VarSize=[1 nVar];   % Decision Variables Matrix Size

VarMin=0;         % Lower Bound of Variables
VarMax=1;         % Upper Bound of Variables

%% CMA-ES Settings

% Maximum Number of Iterations
MaxIt=300;

% Population Size (and Number of Offsprings)
lambda=(4+round(3*log(nVar)))*10;

% Number of Parents
mu=round(lambda/2);

% Parent Weights
w=log(mu+0.5)-log(1:mu);
w=w/sum(w);

% Number of Effective Solutions
mu_eff=1/sum(w.^2);

% Step Size Control Parameters (c_sigma and d_sigma);
sigma0=0.3*(VarMax-VarMin);
cs=(mu_eff+2)/(nVar+mu_eff+5);
ds=1+cs+2*max(sqrt((mu_eff-1)/(nVar+1))-1,0);
ENN=sqrt(nVar)*(1-1/(4*nVar)+1/(21*nVar^2));

% Covariance Update Parameters
cc=(4+mu_eff/nVar)/(4+nVar+2*mu_eff/nVar);
c1=2/((nVar+1.3)^2+mu_eff);
alpha_mu=2;
cmu=min(1-c1,alpha_mu*(mu_eff-2+1/mu_eff)/((nVar+2)^2+alpha_mu*mu_eff/2));
hth=(1.4+2/(nVar+1))*ENN;

%% Initialization

ps=cell(MaxIt,1);
pc=cell(MaxIt,1);
C=cell(MaxIt,1);
sigma=cell(MaxIt,1);

ps{1}=zeros(VarSize);
pc{1}=zeros(VarSize);
C{1}=eye(nVar);
sigma{1}=sigma0;

empty_individual.Position=[];
empty_individual.Step=[];
empty_individual.Cost=[];

M=repmat(empty_individual,MaxIt,1);
M(1).Position=unifrnd(VarMin,VarMax,VarSize);
M(1).Step=zeros(VarSize);
[M(1).Cost,M(1).Sol]=CostFunction(M(1).Position);

BestSol=M(1);

BestCost=zeros(MaxIt,1);

clc;

clear;

close all;

%% Problem Definition

model=CreateModel();

CostFunction=@(xhat) CostFun(xhat,model); % Cost Function

nVar=model.n*(model.n-1)/2; % Number of Decision Variables

VarSize=[1 nVar]; % Decision Variables Matrix Size

VarMin=0; % Lower Bound of Variables

VarMax=1; % Upper Bound of Variables

%% CMA-ES Settings

% Maximum Number of Iterations

MaxIt=300;

% Population Size (and Number of Offsprings)

lambda=(4+round(3*log(nVar)))*10;

% Number of Parents

mu=round(lambda/2);

% Parent Weights

w=log(mu+0.5)-log(1:mu);

w=w/sum(w);

% Number of Effective Solutions

mu_eff=1/sum(w.^2);

% Step Size Control Parameters (c_sigma and d_sigma);

sigma0=0.3*(VarMax-VarMin);

cs=(mu_eff+2)/(nVar+mu_eff+5);

ds=1+cs+2*max(sqrt((mu_eff-1)/(nVar+1))-1,0);

ENN=sqrt(nVar)*(1-1/(4*nVar)+1/(21*nVar^2));

% Covariance Update Parameters

cc=(4+mu_eff/nVar)/(4+nVar+2*mu_eff/nVar);

c1=2/((nVar+1.3)^2+mu_eff);

alpha_mu=2;

cmu=min(1-c1,alpha_mu*(mu_eff-2+1/mu_eff)/((nVar+2)^2+alpha_mu*mu_eff/2));

hth=(1.4+2/(nVar+1))*ENN;

%% Initialization

ps=cell(MaxIt,1);

pc=cell(MaxIt,1);

C=cell(MaxIt,1);

sigma=cell(MaxIt,1);

ps{1}=zeros(VarSize);

pc{1}=zeros(VarSize);

C{1}=eye(nVar);

sigma{1}=sigma0;

empty_individual.Position=[];

empty_individual.Step=[];

empty_individual.Cost=[];

M=repmat(empty_individual,MaxIt,1);

M(1).Position=unifrnd(VarMin,VarMax,VarSize);

M(1).Step=zeros(VarSize);

[M(1).Cost,M(1).Sol]=CostFunction(M(1).Position);

BestSol=M(1);

BestCost=zeros(MaxIt,1);

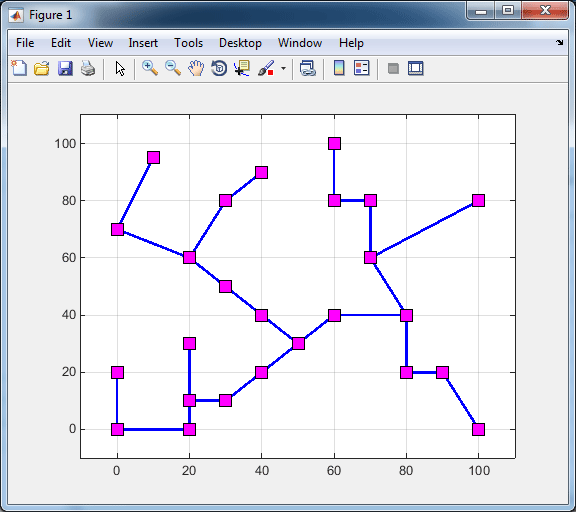
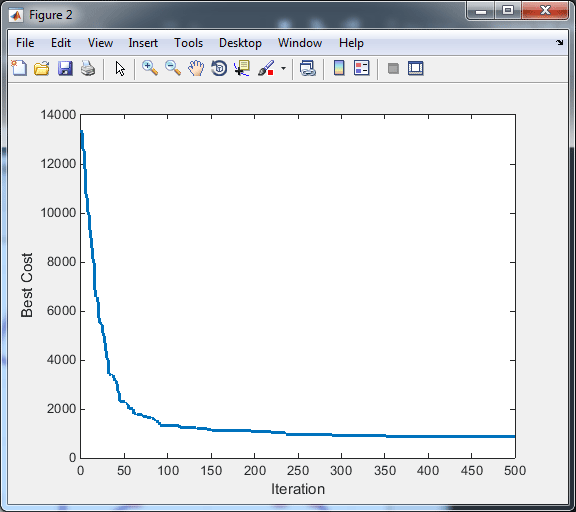
تصاویر خروجی محصول

درخت پوشای مینیمم با الگوریتم CMAES

ویدئوی معرفی محصول

درباره محصول

سورس کد تعیین درخت پوشای مینیمم با الگوریتم CMAES در متلب در محیط Matlab 2014b نوشته و اجرا شده است این سورس کد توسط تیم پشتیبانی پی استور تست و اجرا شده است. کیفیت محصول توسط پی استور تضمین می شود و محصول دارای نشان تضمین کیفیت پی استور می باشد. برای دانلود محصول آن را خریداری فرمایید به محض خرید لینک دانلود در دسترس خواهد بود.

1 دیدگاه برای تعیین درخت پوشای مینیمم با الگوریتم CMAES در متلب

امتیاز 5 از 5
programstore – ۱۳۹۸/۰۴/۱۴
نظرات و پیشنهادات خود را با ما در میان بگذارید.
برای پاسخ وارد شوید

دیدگاه خود را بنویسید

این سایت از اکیسمت برای کاهش هرزنامه استفاده می کند. بیاموزید که چگونه اطلاعات دیدگاه های شما پردازش می‌شوند.

اطلاعات فروشنده

نام فروشگاه: پی استور
فروشنده: پی استور
آدرس: خیابان فردوس - بن بست فردوس 1 - پلاک 105
آذربایجان شرقی
5451358816
4.94 4.94 امتیاز از 216 دیدگاه

تعیین درخت پوشای مینیمم با الگوریتم CMAES در متلب