مقایسه الگوریتم های حل مسئله TSP
در این پست سورس کد مقایسه الگوریتم های حل مسئله TSP قرار داده شده است. برای حل مسئله TSP یا همان فروشنده دوره گرد Traveling Salesman Problem می توان از الگوریتم های بهینه سازی یا فراابتکاری (Metaheuristic) استفاده کرد. هدف از الگوریتم های بهینه سازی يافتن یک جواب قابل قبول، با توجه به محدوديت و نياز مسئله است. در ادامه توضیحات کامل تری ارائه می شود.
مقایسه الگوریتم ها
در سورس کدی که در متلب برای شما آماده شده است به مقایسه 12 الگوریتم بهینه سازی برای حل مسئله TSP و نتایج حاصل از آنها پرداخته شده است. این الگوریتم ها مبتنی بر جمعیت یا population based بوده که با الهام گیری از طبیعت و محیط پیرامون ما اقدام به حل مسئله می کنند. این الگوریتم ها عبارتند از:
- الگوریتم ژنتیک GA
- الگوریتم ازدحام ذرات PSO
- الگوریتم کلونی مورچگان ACO
- الگوریتم زنبور عسل مصنوعی BEE
- الگوریتم استراتژی تکاملی انطباق ماتریس کوواریانس CMA-ES
- الگوریتم تفاضل تکاملی DE
- الگوریتم کرم شب تاب FA
- الگوریتم جهش قورباغه SFLA
- الگوریتم رقابت استعماری ICA
- الگوریتم گرگ خاکستری GWO
- الگوریتم وال یا نهنگ WOA
- الگوریتم شمع و پروانه MFO
برای مقایسه عملکرد الگوریتم های فوق بر روی مسئله TSP از یک مدل سازی پیوسته برای جایکشت های شهر ها استفده شده است. با اجرای سورس کد 2 خروجی خواهیم داشت یکی موقعیت شهرها و نحوه حرکت فروشنده دوره گرد و دیگری نمودار همگرایی.
مسئله فروشنده دورگرد TSP
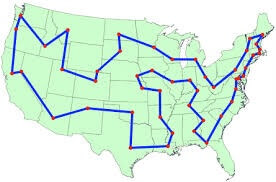
مساله فروشنده دوره گرد Travelling salesman problem یا به اختصار TSP مساله اي است که شرح آن خيلي آسان مي باشد. تعريف آن بدين صورت است که تعداد متناهي شهر با هزينه پيمايش بين هر جفت از آنها داده مي شود و هدف مساله اين است که يک فروشنده دوره گرد تمامي اين شهرها را به گونه اي ملاقات کند که هر يک از اين شهرها را فقط يک بارملاقات کرده و دوباره به شهر آغازين برگردد با اين شرط که با کمترين هزينه پيمايش اين کار را انجام دهد.
به طور کلي هدف پيدا کردن کم هزينه ترين تور براي پیمایش همه شهرها و بازگشت به شهر آغازين حرکت است. مساله فروشنده دوره گرد در شکل ساده و اختصاري با نام TSP شناخته مي شود. شکل زیر يک نمونه جواب از مساله فروشنده دوره گرد که در سال 1591 براي 15 شهر از کشور آمريکا مطرح شد را نشان مي دهد که با روش شاخه و حد حل شد.
قسمتی از سورس کد
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
clc close all clear addpath('GA'); addpath('PSO'); addpath('ACO'); addpath('BEE'); addpath('CMA-ES'); addpath('DE'); addpath('FA'); addpath('GWO'); addpath('ICA'); addpath('SFLA'); addpath('WOA'); addpath('MFO'); model=CreateModel(); dim=model.n; lb=0; ub=1; fobj=@(tour) TourLength(tour,model); SearchAgents_no=50; % Number of search agents Max_iteration=1000; % Maximum numbef of iterations Positions=initialization(SearchAgents_no,dim,ub,lb); [Best_SolGA,GA_cg_curve]=GA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_SolPSO,PSO_cg_curve]=PSO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_SolACO,ACO_cg_curve]=ACO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_SolBEE,BEE_cg_curve]=BEE(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_Solcmaes,cmaes_cg_curve]=cmaes(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_SolDE,DE_cg_curve]=DE(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_SolFA,FA_cg_curve]=FA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_SolICA,ICA_cg_curve]=ICA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_SolSFLA,SFLA_cg_curve]=SFLA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_scoreGWO,Best_posGWO,GWO_cg_curve]=GWO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_scoreWOA,Best_posWOA,WOA_cg_curve]=WOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); [Best_scoreMFO,Best_posMFO,MFO_cg_curve]=MFO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Positions); figure(1); %Draw objective space semilogy(GA_cg_curve,'Color','[0 0 0]','LineWidth',2) hold on; semilogy(PSO_cg_curve,'Color','[0 0 1]','LineWidth',2) semilogy(ACO_cg_curve,'Color','[0 1 0]','LineWidth',2) semilogy(BEE_cg_curve,'Color','[0 1 1]','LineWidth',2) semilogy(cmaes_cg_curve,'Color','[1 0 0]','LineWidth',2) semilogy(DE_cg_curve,'Color','[1 0 1]','LineWidth',2) semilogy(FA_cg_curve,'Color','[1 1 0]','LineWidth',2) semilogy(ICA_cg_curve,'--','Color','[0 0 1]','LineWidth',2) semilogy(SFLA_cg_curve,'--','Color','[0 1 0]','LineWidth',2) semilogy(GWO_cg_curve,'--','Color','[0 1 1]','LineWidth',2) semilogy(WOA_cg_curve,'--','Color','[1 0 0]','LineWidth',2) semilogy(MFO_cg_curve,'--','Color','[1 0 1]','LineWidth',2) xlabel('Iteration'); ylabel('Best score obtained so far'); grid on legend('GA','PSO','ACO','BEE','CMA-ES','DE','FA','ICA','SFLA','GWO','WOA','MFO','Location','bestoutside') test; |
برای دریافت سورس کامل مقایسه الگوریتم های حل مسئله TSP محصول لطفا آن را خریداری کنید.
تصاویر خروجی پروژه
ویدئوی معرفی پروژه
درباره محصول
سورس کد مقایسه الگوریتم های حل مسئله TSP برای حل مسئله فروشنده دوره گرد TSP با الگوریتم های بهینه سازی یا فرا ابتکاری در متلب عنوان محصولی است که در این پست به آن پرداخته شده است. محصول در نرم افزار متلب 2017 نوشته شده و بصورت کامل توسط گروه پشتیبانی پی استور تست و اجرا شده است. محصول دارای نشان تضمین کیفیت پی استور می باشد. برای دانلود محصول آن را خریداری کنید.
قوانین ثبت دیدگاه
- دیدگاه های فینگلیش تایید نخواهند شد.
- دیدگاه های نامرتبط به مطلب تایید نخواهد شد.
- از درج دیدگاه های تکراری پرهیز نمایید.
- امتیاز دادن به محصول فقط مخصوص خریداران آن می باشد.
اطلاعات فروشنده
- نام فروشگاه: پی استور
- فروشنده: امین جلیل زاده رزین
- آدرس: آذربایجان شرقی
- 4.93 امتیاز از 374 دیدگاه
آموزش شبکه عصبی با الگوریتم ژنتیک GA در متلب
این فایل به زبان Matlab و بصورت zip شده قابل دانلود است. بلافاصله پس از خرید، لینک دانلود محصول در اختیار شما قرار خواهد گرفت.
با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:
- دسترسی به فایل محصول به صورت مادام‌العمر
- ۶ ماه پشتیبانی کاملا رایگان و تضمین شده
پروژه اتاق سه بعدی با در و پنجره و میز و قوری در OpenGl
این فایل در OpenGl و با ++Visual C طراحی شده است. بلافاصله پس از خرید، لینک دانلود محصول در اختیار شما قرار خواهد گرفت.
با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:
- دسترسی به فایل محصول به صورت مادام‌العمر
- ۶ ماه پشتیبانی کاملا رایگان و تضمین شده
سورس کد الگوریتم مورچه ACO برای حل مسئله کوله پشتی Knapsack در متلب
سورس برنامه در نرم افزار متلب نوشته شده است و بلافاصله پس از خرید، لینک دانلود در اختیار شما قرار خواهد گرفت.
با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:
- دسترسی به فایل محصول به صورت مادام‌العمر
- ۶ ماه پشتیبانی کاملا رایگان و تضمین شده
ترجمه مفهومی مقاله خوشه بندی نابرابر مبتنی بر تئوری فازی در شبکه های حسگر بی سیم
این فایل بصورت word در 14 صفحه می باشد. بلافاصله پس از خرید، لینک دانلود محصول در اختیار شما قرار خواهد گرفت.
با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:
- دسترسی به فایل محصول به صورت مادام‌العمر
- ۶ ماه پشتیبانی کاملا رایگان و تضمین شده
سمینار روش های پیش بینی و تخمین نقص نرم افزار با استفاده از داده کاوی
این سمینار در 37 صفحه در قالب word و pdf بصورت زیپ شده قابل دانلود است. به محض خرید محصول لینک دانلود در دسترس خواهد بود.
با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:
- دسترسی به فایل محصول به صورت مادام‌العمر
- ۶ ماه پشتیبانی کاملا رایگان و تضمین شده
ترجمه مقاله رویکرد تکاملی جدید برای مشکل خوشه بندی متعادل بار در شبکه های حسگر بی سیم
ترجمه این مقاله در 17 صفحه در قالب pdf بصورت زیپ شده قابل دانلود است. به محض خرید محصول لینک دانلود در دسترس خواهد بود.
با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:
- دسترسی به فایل محصول به صورت مادام‌العمر
- ۶ ماه پشتیبانی کاملا رایگان و تضمین شده
محصولات مشابه
قیمت 35,000 تومان
امین جلیل زاده(مدیریت)
نظرات و پیشنهادات خود را با ما در میان بگذارید.