در این پست به مسئله حل درخت پوشای مینیمم با الگوریتم رقابت استعماری در متلب پرداخته شده است. درخت پوشای مینیمم یا درخت پوشای کمینه درختی است از زیر مجموعه ای از گراف G که تمام رأس ها با حداقل تعداد ممکن لبه ها پوشیده شده است که دارای حداقل هزینه باشد. از این رو، در درخت پوشای مینیمم حلقه ای وجود ندارد و همچنین نمی تواند قطع باشد.
الگوریتم رقابت استعماری یا Imperialist Competitive algorithm که به اختصار ICA نامیده می شود جزو الگوریتم های تکاملی یا فرا ابتکاری هستند که به یافتن پاسخ بهینه مسائل مختلف بهینه سازی میپردازد. این الگوریتم با مدل سازی ریاضی فرایند تکامل اجتماعی – سیاسی، الگوریتمی برای حل مسائل ریاضی بهینهسازی ارائه میدهد. در این پست با استفاده از فرآیند تولید جواب الگوریتم رقابت استعماری مسئله درخت پوشای کمینه در نرم افزار متلب ارائه شده است.

برنامهنویس: تیم برنامه نویسی پی استور
متشکل از اساتید و فارغ التحصیلان رشته های فنی - مهندسی
تیم برنامه نویسی پی استور یکی از اولین گروه های تشکیل شده در مجموعه آموزشی پی استور می باشد. این تیم از اساتید مجرب و فارغ التحصیلان رشته های فنی و مهندسی تشکیل شده که در زمینه های مختلف برنامه نویسی و تهیه سورس کد فعال هستند.
درخت پوشای کمینه (مینیمم)
با توجه به یک گراف متصل و بدون جهت، درخت پوشا از آن گراف یک زیرگرافی است که اولاً یک درخت است و تمام رأس ها را با یکدیگر متصل می کند. یک گراف می تواند انواع درخت های مختلف را پوشش دهد. یک Minimum Spanning Tree درخت پوشای کمینه (MST) یا درخت پوشای مینیمال برای یک گراف وزنم دار، متصل و بدون جهت یک درخت پوشا با وزن کمتر یا برابر با وزن هر درخت دیگر است. وزن یک درخت، مجموع وزن های داده شده به هر لبه درخت است.
الگوریتم رقابت استعماری Imperialist Competitive algorithm
الگوریتم رقابت استعماری ICA روشی در حوزه محاسبات تکاملی است که به یافتن پاسخ بهینه مسائل مختلف بهینه سازی میپردازد. این الگوریتم با مدل سازی ریاضی فرایند تکامل اجتماعی – سیاسی، الگوریتمی برای حل مسائل ریاضی بهینهسازی ارائه میدهد ازلحاظ کاربرد، این الگوریتم در دسته الگوریتمهای بهینهسازی تکاملی همچون الگوریتم های ژنتیک روش بهینهسازی ازدحام ذرات، الگوریتم کلونی مورچگان، الگوریتم تبرید شبیهسازی شده و … قرار می گیرد.
همانند همه الگوریتمهای قرارگرفته در این دسته، الگوریتم رقابت استعماری نیز مجموعه اولیهای از جواب های احتمالی را تشکیل می دهد. این جواب های اولیه در الگوریتم ژنتیک با عنوان کروموزوم، در الگوریتم ازدحام ذرات با عنوان ذره و در الگوریتم رقابت استعماری نیز با عنوان کشور شناخته میشوند. الگوریتم رقابت استعماری با روند خاصی که در ادامه آمده است، این جواب های اولیه (کشورها) را بهتدریج بهبود داده و درنهایت جواب مناسب مسئله بهینه سازی را در اختیار میگذارد.
مراحل کلی روند الگوریتم بهصورت زیر است.
1- چند نقطه تصادفی روی تابع انتخاب کرده و امپراتوریهای اولیه را تشکیل بده.
2- مستعمرات را به سمت کشور امپریالیست حرکت بده (سیاست همسانسازی یا جذب).
3- عملگر انقلاب را اعمال کن.
4- اگر مستعمرهای در یک امپراتوری وجود داشته باشد که هزینه¬ای کمتر از امپریالیست داشته باشد جای مستعمره و امپریالیست را عوض کن.
5- هزینه کل یک امپراتوری را حساب کن (با در نظر گرفتن هزینه امپریالیست و مستعمراتشان).
6- یک (چند) مستعمره از ضعیفترین امپراتوری را انتخاب کرده و آن را به امپراتوری که بیشترین احتمال تصاحب را دارد، بده.
7- امپراتوریهای ضعیف را حذف کن.
8- اگر تنها یک امپراتوری باقیمانده باشد توقف کن و در غیر این صورت به 2 برو.
فلوچارت الگوریتم رقابت استعماری بصورت زیر است.
قسمتی از سورس محصول
% ICA Parameters MaxIt=500; % Maximum Number of Iterations nPop=300; % Population Size nEmp=10; % Number of Empires/Imperialists alpha=1; % Selection Pressure beta=2; % Assimilation Coefficient pRevolution=0.5; % Revolution Probability mu=0.1; % Revolution Rate zeta=0.1; % Colonies Mean Cost Coefficient %% Share (Globalize) Settings global ProblemSettings; ProblemSettings.CostFunction=CostFunction; ProblemSettings.nVar=nVar; ProblemSettings.VarSize=VarSize; ProblemSettings.VarMin=VarMin; ProblemSettings.VarMax=VarMax; global ICASettings; ICASettings.MaxIt=MaxIt; ICASettings.nPop=nPop; ICASettings.nEmp=nEmp; ICASettings.alpha=alpha; ICASettings.beta=beta; ICASettings.pRevolution=pRevolution; ICASettings.mu=mu; ICASettings.zeta=zeta; %% Initialization % Initialize Empires emp=CreateInitialEmpires(); % Array to Hold Best Cost Values BestCost=zeros(MaxIt,1); %% ICA Main Loop for it=1:MaxIt % Assimilation emp=AssimilateColonies(emp); % Revolution emp=DoRevolution(emp); % Intra-Empire Competition emp=IntraEmpireCompetition(emp); % Update Total Cost of Empires emp=UpdateTotalCost(emp); % Inter-Empire Competition emp=InterEmpireCompetition(emp); % Update Best Solution Ever Found imp=[emp.Imp]; [~, BestImpIndex]=min([imp.Cost]); BestSol=imp(BestImpIndex); % Update Best Cost BestCost(it)=BestSol.Cost; % Show Iteration Information if BestSol.Sol.IsFeasible Flag=' *'; else Flag=[', DC = ' num2str(BestSol.Sol.q)]; end disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it)) Flag]); % Plot Best Solution figure(1); PlotSolution(BestSol.Sol,model); pause(0.01); end
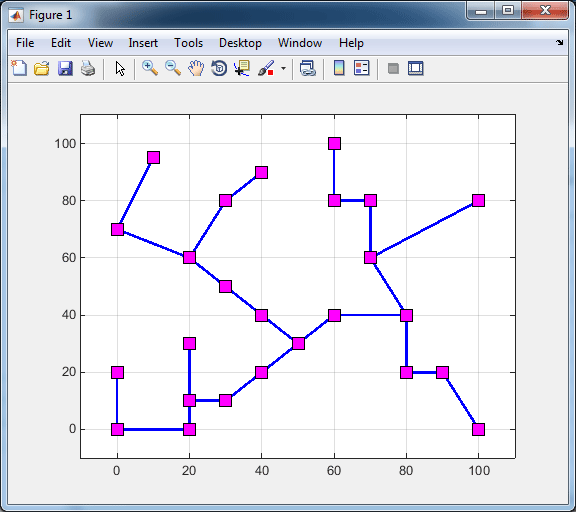
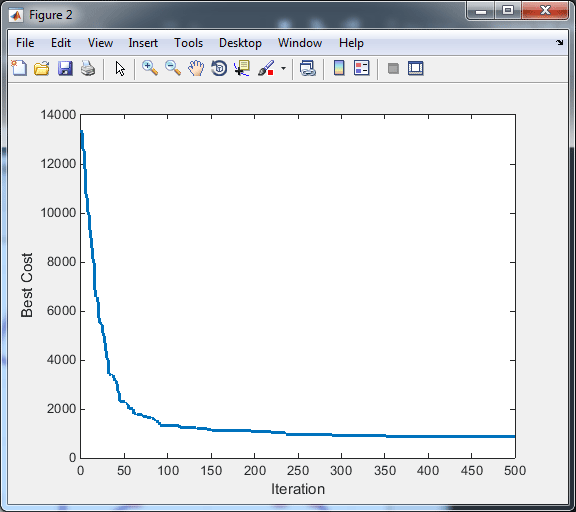
تصاویر خروجی محصول
ویدئوی معرفی محصول
درباره محصول
سورس کد تعیین درخت پوشای مینیمم با الگوریتم رقابت استعماری در متلب در محیط Matlab 2014b نوشته و اجرا شده است این سورس کد توسط تیم پشتیبانی پی استور تست و اجرا شده است. کیفیت محصول توسط پی استور تضمین می شود و محصول دارای نشان تضمین کیفیت پی استور می باشد. برای دانلود محصول آن را خریداری فرمایید به محض خرید لینک دانلود در دسترس خواهد بود.
مباحث مرتبط با این موضوع
مباحث مرتبط با الگوریتم های تعیین درخت پوشای مینیمم
تعیین درخت پوشای مینیمم با الگوریتم رقابت استعماری در متلب
| تاریخ انتشار: | 14 اسفند 1397 |
|---|---|
| تاریخ بروزرسانی: | 20 خرداد 1398 |
| حجم فایل: | 7 کیلوبایت |
| فرمت فایل | m. در قالب متلب |
| مدت زمان: | 1.0 |
| شناسه اثر: | ندارد |
| هماهنگی با: | Matlab 2014b |
تاکنون 465 نفر این محصول را تهیه کرده اند و 1 نظر برای آن ثبت شده است.
نظرات و دیدگاه ها
قوانین ثبت دیدگاه
- لطفاً دیدگاه های خود را فارسی تایپ کنید.
- دیدگاه های نامرتبط به مطلب تایید نخواهد شد.
- از درج دیدگاه های تکراری پرهیز نمایید.
- سوالات تخصصی خودتان را از طریق تیکت پشتیبانی مطرح کنید.
تعیین درخت پوشای مینیمم با الگوریتم رقابت استعماری در متلب
هزینه سفارش: 99,000 تومان
با تخفیف 40 درصدی: فقط 59,400 تومان
| تاریخ انتشار: | 14 اسفند 1397 |
|---|---|
| تاریخ بروزرسانی: | 20 خرداد 1398 |
| حجم فایل: | 7 کیلوبایت |
| فرمت فایل | m. در قالب متلب |
| مدت زمان: | 1.0 |
| شناسه اثر: | ندارد |
| هماهنگی با: | Matlab 2014b |
1 بازخورد (مشاهده نظرات)
هزینه سفارش: 99,000 تومان









علی
سلام برای جستجوی گرانشی فایلش رو دارید؟
مدیریت و پشتیبانی
سلام بله هست ولی این الگوریتم روی مسئله درخت پوشا جواب خوبی نمی ده ولی اگه خواستین با ما در ارتباط باشید.