سورس کد الگوریتم رقابت استعماری برای حل مسئله فروشنده دوره گرد TSP در متلب عنوان موضوعی است که در این پست به آن پرداخته می شود. الگوریتم رقابت استعماری با نام Imperialist Competitive Algorithm یا الگوریتم ICA نیز نامیده می شود. در این مجموعه سعی می کنیم تا جزئیات بهتری از سورس کد الگوریتم رقابت استعماری فروشنده دوره گرد در متلب ICA ارائه دهیم.

برنامهنویس: تیم برنامه نویسی پی استور
متشکل از اساتید و فارغ التحصیلان رشته های فنی - مهندسی
تیم برنامه نویسی پی استور یکی از اولین گروه های تشکیل شده در مجموعه آموزشی پی استور می باشد. این تیم از اساتید مجرب و فارغ التحصیلان رشته های فنی و مهندسی تشکیل شده که در زمینه های مختلف برنامه نویسی و تهیه سورس کد فعال هستند.
الگوریتم رقابت استعماری (ICA)
همانند همه الگوریتمهای قرار گرفته در دسته الگوریتم های بهینه سازی، الگوریتم رقابت استعماری نیز مجموعه اولیه ای از جوابهای احتمالی را تشکیل میدهد. این جواب های اولیه در الگوریتم ژنتیک با عنوان «کروموزوم»، در الگوریتم ازدحام ذرات با عنوان «ذره» و در الگوریتم رقابت استعماری نیز با عنوان «کشور» شناخته میشوند. الگوریتم رقابت استعماری با روند خاصی که در ادامه میآید، این جوابهای اولیه (کشورها) را به تدریج بهبود داده و در نهایت جواب مناسب مسئله بهینهسازی (کشور مطلوب) را در اختیار میگذارد.
پایههای اصلی این الگوریتم را سیاست همسان سازی (Assimilation)، رقابت استعماری (Imperialistic Competition) و انقلاب (Revolution) تشکیل میدهند. این الگوریتم با تقلید از روند تکامل اجتماعی، اقتصادی و سیاسی کشورها و با مدلسازی ریاضی بخشهایی از این فرایند، عملگرهایی را در قالب منظم به صورت الگوریتم ارائه میدهد که میتوانند به حل مسائل پیچیده بهینهسازی کمک کنند.
در واقع این الگوریتم جوابهای مسئله بهینهسازی را در قالب کشورها نگریسته و سعی میکند در طی فرایندی تکرار شونده این جوابها را رفته رفته بهبود داده و در نهایت به جواب بهینه مسئله برساند.
مراحل الگوریتم رقابت استعماری
مراحل کلی روند الگوریتم بهصورت زیر است.
- چند نقطه تصادفی روی تابع انتخاب کرده و امپراتوریهای اولیه را تشکیل بده.
- مستعمرات را به سمت کشور امپریالیست حرکت بده (سیاست همسانسازی یا جذب).
- عملگر انقلاب را اعمال کن.
- اگر مستعمرهای در یک امپراتوری وجود داشته باشد که هزینه ای کمتر از امپریالیست داشته باشد جای مستعمره و امپریالیست را عوض کن.
- هزینه کل یک امپراتوری را حساب کن (با در نظر گرفتن هزینه امپریالیست و مستعمراتشان).
- یک (چند) مستعمره از ضعیفترین امپراتوری را انتخاب کرده و آن را به امپراتوری که بیشترین احتمال تصاحب را دارد، بده.
- امپراتوریهای ضعیف را حذف کن.
- اگر تنها یک امپراتوری باقیمانده باشد توقف کن و در غیر این صورت به 2 برو.
برای درک کامل الگوریتم الگوریتم رقابت استعماری مقاله ای تحت عنوان الگوریتم رقابت استعماری IMPERIALIST COMPETITIVE ALGORITHM آماده کرده ایم که می توانید مطالعه کنید.
مسئله فروشنده دورگرد TSP
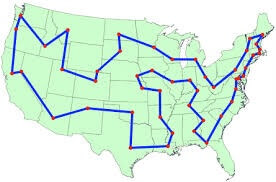
مساله فروشنده دوره گرد Travelling salesman problem یا به اختصار TSP مساله اي است که شرح آن خيلي آسان مي باشد. تعريف آن بدين صورت است که تعداد متناهي شهر با هزينه پيمايش بين هر جفت از آنها داده مي شود و هدف مساله اين است که يک فروشنده دوره گرد تمامي اين شهرها را به گونه اي ملاقات کند که هر يک از اين شهرها را فقط يک بارملاقات کرده و دوباره به شهر آغازين برگردد با اين شرط که با کمترين هزينه پيمايش اين کار را انجام دهد.
به طور کلي هدف پيدا کردن کم هزينه ترين تور براي ملاقات همه شهرها و بازگشت به شهر آغازين حرکت است. مساله فروشنده دوره گرد در شکل ساده و اختصاري با نام TSP شناخته مي شود. شکل 3- 1 يک نمونه جواب از مساله فروشنده دوره گرد که در سال 1591 براي 15 شهر از کشور آمريکا مطرح شد را نشان مي دهد که با روش شاخه وحد حل شد.
سورس حل مسئله فروشنده دوره گرد TSP با الگوریتم ICA در متلب
در این قسمت سورس برنامه حل مسئله فروشنده دوره گرد TSP با الگوریتم ICA در متلب آماده شده است این سورس کد شامل 13 فایل می باشد که عبارتند از:
- TSPICA.m: فایل اصلی برنامه است و فراخوانی دیگر توابع و مقادیر پارامتر ها و الگوریتم ICA در داخل این فایل قرار دارد.
- CreateModel.m: برای ایجاد شهرهای فاصله و مختصات هر یک از شهرها از این تابع استفاده می شود.
function model=CreateModel()
x=[82 91 12 92 63 9 28 55 96 97 15 98 96 49 12 92 63 9 28 55 96 97 15 98 80 14 42 92 80 96];
y=[12 92 63 9 28 55 96 97 15 98 66 3 85 94 68 76 75 39 66 17 71 3 27 4 9 83 70 32 95 3];
n=numel(x);
D=zeros(n,n);
for i=1:n-1
for j=i+1:n
D(i,j)=sqrt((x(i)-x(j))^2+(y(i)-y(j))^2);
D(j,i)=D(i,j);
end
end
model.n=n;
model.x=x;
model.y=y;
model.D=D;
end
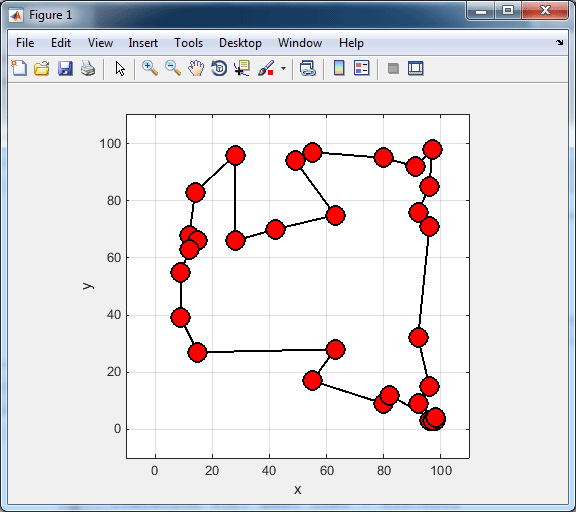
PlotSolution.m: برای رسم مسیر های بین شهرها از این تابع استفاده می شود.
function PlotSolution(tour,model)
tour=[tour tour(1)];
plot(model.x(tour),model.y(tour),'k-s',...
'MarkerSize',12,...
'MarkerFaceColor','y',...
'LineWidth',2);
end
- MyCost.m: این تابع برای محاسبه طول مسیرهای یک تور یا یک پیمایش کامل شهرها بکار می رود.
function [z sol]=MyCost(s,model)
d=model.d;
[~, tour]=sort(s);
sol.tour=tour;
n=numel(tour);
tour=[tour tour(1)];
L=0;
for i=1:n
L=L+d(tour(i),tour(i+1));
end
sol.L=L;
z=L;
end
برای دریافت سورس کامل محصول لطفا آن را خریداری کنید.
تصاویر خروجی محصول
ویدئوی معرفی محصول
درباره الگوریتم رقابت استعماری فروشنده دوره گرد
سورس برنامه حل مسئله فروشنده دوره گرد TSP با الگوریتم رقابت استعماری ICA در متلب عنوان محصولی است که در این پست به آن پرداخته شده است. محصول در نرم افزار متلب نوشته شده و بصورت کامل توسط گروه پشتیبانی پی استور تست و اجرا شده است. محصول دارای نشان تضمین کیفیت پی استور می باشد. برای دانلود محصول آن را خریداری کنید.
مباحث مرتبط با الگوریتم رقابت استعماری
سورس کدهای حل مسئله فروشنده دوره گرد
الگوریتم رقابت استعماری فروشنده دوره گرد – الگوریتم رقابت استعماری برای حل مسئله فروشنده دوره گرد TSP در متلب
| تاریخ انتشار: | 25 تیر 1398 |
|---|---|
| تاریخ بروزرسانی: | 25 بهمن 1398 |
| حجم فایل: | 5 کیلوبایت |
| فرمت فایل | m. در قالب متلب |
| مدت زمان: | 1.0 |
| شناسه اثر: | ندارد |
| هماهنگی با: | Matlab 2009 و بالاتر |
تاکنون 587 نفر این محصول را تهیه کرده اند و 1 نظر برای آن ثبت شده است.
نظرات و دیدگاه ها
قوانین ثبت دیدگاه
- لطفاً دیدگاه های خود را فارسی تایپ کنید.
- دیدگاه های نامرتبط به مطلب تایید نخواهد شد.
- از درج دیدگاه های تکراری پرهیز نمایید.
- سوالات تخصصی خودتان را از طریق تیکت پشتیبانی مطرح کنید.
الگوریتم رقابت استعماری فروشنده دوره گرد – الگوریتم رقابت استعماری برای حل مسئله فروشنده دوره گرد TSP در متلب
هزینه سفارش: 129,000 تومان
| تاریخ انتشار: | 25 تیر 1398 |
|---|---|
| تاریخ بروزرسانی: | 25 بهمن 1398 |
| حجم فایل: | 5 کیلوبایت |
| فرمت فایل | m. در قالب متلب |
| مدت زمان: | 1.0 |
| شناسه اثر: | ندارد |
| هماهنگی با: | Matlab 2009 و بالاتر |
1 بازخورد (مشاهده نظرات)
هزینه سفارش: 129,000 تومان











مدیریت و پشتیبانی
نظرات و پیشنهادات خود را با ما در میان بگذارید.