Name: الگوریتم جستجوی ممنوعه TS برای حل مسئله فروشنده دوره گرد TSP در متلب
Brand: پی استور
SKU: 4665
Price: 18000 IRT
Availability: instock
Rating: 5.00 (1 reviews)

سورس کد الگوریتم جستجوی ممنوعه TS برای حل مسئله فروشنده دوره گرد TSP در متلب

در این پست پیاده سازی الگوریتم جستجوی ممنوعه TS برای حل مسئله فروشنده دوره گرد TSP در متلب قرار داده شده است. واژهٔ ممنوعه یا تابو از تُنگان زبان مردم جزایر پلینزی در اقیانوس آرام گرفته شده‌است. این واژه به معنای شیء مقدسی است که به دلیل قداست نباید آن را لمس کرد. بر اساس واژه‌نامهٔ وِبستر، امروزه این واژه در معنای «ممنوعیت ایجاد شده به دلیل فرهنگ اجتماعی برای ایجاد اقدام حفاظتی» یا «ممنوعیت چیزی که دارای ریسک است»، به کار می‌رود. معنای اخیر واژهٔ تابو، با تکنیک جستجوی ممنوعه کاملاً سازگار است. ریسکی که در الگوریتم جستجوی ممنوعه از آن اجتناب می‌شود، خطر مسیرهای نامناسب است. در ادامه به توضیح این الگوریتم و سورس کد آن پرداخته می شود.

الگوریتم جستجوی ممنوعه (Tabu Search) (TS)

الگوریتم جستجوی ممنوعه (Tabu Search) (TS) یک استراتژی جستجوی حافظه ای می باشد که برای اولین بار توسط گلوور در سال 1986 مطرح شده است. این الگوریتم تقریبا مانند الگوریتم های جستجوی محلی کار می کند، با این تفاوت که برای جلوگیری از دور و تسلسل در جواب ها و افتادن در دام جوا ب های بهینه محلی، از مفهومی به نام فهرست ممنوع استفاده می کند. جابه جایی از جواب جاری به جواب همسایه امکان پذیر زمانی انجام می شود که در فهرست تابو قرار نداشته باشد. در غیر اینصورت، جواب همسایه دیگری که در ارزیابی جواب های همسایه در رده بعدی قرار گرفته است، انتخاب شده و جابه جایی به آن صورت م یگیرد. هرگاه ساختار همسایگی متقارن باشد، خطر افتادن در دور وجود دارد. نمودار جریان الگوریتم جستجوی ممنوعه بصورت زیر است.

الگوریتم جستجوی ممنوعه

حافظه الگوریتم میتواند از دو نوع recency و یا frequency باشد

حافظه recency :

حافظه کوتاه مدت در روش جستجوی ممنوع نوعی از جستجوی فعال را جهت یافتن بهترین جواب ها تشکیل می دهد و می توان اینگونه بیان نمود که هسته اصلی جستجوی ممنوع، در فرایند کوتاه مدت مجسم می شود. این حافظه لیستی با ابعاد N رکورد می باشد که N تا از آخرین حرکاتی را که الگوریتم با آن مواجه بوده است را به عنوان tabu نگهداری میکند.

حافظه frequency :

حافظه frequency که به عنوان حافظه بلندمدت شناخته می شود با اضافه نمودن اطلاعات تکمیلی دیگری از قبیل اینکه چند بار یک حرکت و یا جواب ممنوع جستجو شده است، مکمل حافظه recency می باشد. در حالت کلی جستجوی ممنوع با در نظر گرفتن حافظه بلند مدت و استراتژی های مرتبط با آن قوی تر میشود.

لیست ممنوع یا Tabu:

این لیست که دارای ابعادی ثابت یا متغیر می باشد، جابه جایی های منع شده را نگهداری می کند و کاربرد اصلی آن، پرهیز از همگرا شدن به جواب های بهینه محلی است. به عبارت دیگر، به کمک فهرست tabu جابه جایی به جوا بهایی که اخیراً جستجو شده اند، ممنوع خواهد شد و فقط بخش هایی از مجموعه جواب که پیش از این مورد بررسی قرار نگرفته، مد نظر خواهند بود. نحوه ورود و خروج جواب ها به فهرست ممنوع به صورت FIFO است.

مسئله فروشنده دورگرد TSP

مساله فروشنده دوره گرد Travelling salesman problem یا به اختصار TSP مساله اي است که شرح آن خيلي آسان مي باشد. تعريف آن بدين صورت است که تعداد متناهي شهر با هزينه پيمايش بين هر جفت از آنها داده مي شود و هدف مساله اين است که يک فروشنده دوره گرد تمامي اين شهرها را به گونه اي ملاقات کند که هر يک از اين شهرها را فقط يک بارملاقات کرده و دوباره به شهر آغازين برگردد با اين شرط که با کمترين هزينه پيمايش اين کار را انجام دهد.

فروشنده دوره گرد TSP

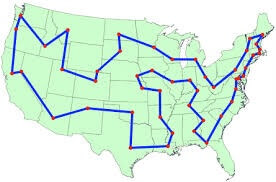
به طور کلي هدف پيدا کردن کم هزينه ترين تور براي ملاقات همه شهرها و بازگشت به شهر آغازين حرکت است. مساله فروشنده دوره گرد در شکل ساده و اختصاري با نام TSP شناخته مي شود. شکل زیر يک نمونه جواب از مساله فروشنده دوره گرد که در سال 1591 براي 15 شهر از کشور آمريکا مطرح شد را نشان مي دهد که با روش شاخه وحد حل شد.

سور س حل مسئله فروشنده دوره گرد TSP با الگوریتم TS در متلب

در این بخش قسمتی از سورس برنامه حل مسئله فروشنده دوره گرد TSP با الگوریتم TS در متلب آماده شده است این سورس کد شامل 10 فایل می باشد که عبارتند از:

الگوریتم جستجوی ممنوعه

قسمتی از کد TabuSearch به صورت زیر است:

model = CreateModel();

CostFunction=@(tour) TourLength(tour, model); 

ActionList=CreatePermActionList(model.n);

nAction=numel(ActionList);     


%% Parameters

MaxIt=100;                     

TL=round(0.5*nAction);     


%% Initialization


empty_individual.Position=[];
empty_individual.Cost=[];

% Create Initial Solution
sol=empty_individual;
sol.Position=randperm(model.n);
sol.Cost=CostFunction(sol.Position);

% Initialize Best Solution Ever Found
BestSol=sol;

% Array to Hold Best Costs
BestCost=zeros(MaxIt,1);

% Initialize Action Tabu Counters
TC=zeros(nAction,1);


%% Main Loop

for it=1:MaxIt
    
    bestnewsol.Cost=inf;
    
    % Apply Actions
    for i=1:nAction
        if TC(i)==0
            newsol.Position=Action(sol.Position,ActionList{i});
            newsol.Cost=CostFunction(newsol.Position);
            newsol.ActionIndex=i;

            if newsol.Cost&lt;=bestnewsol.Cost
                bestnewsol=newsol;
            end
        end
    end
    
    % Update Current Solution
    sol=bestnewsol;
    
    % Update Tabu List
    for i=1:nAction
        if i==bestnewsol.ActionIndex
            TC(i)=TL;               % Add To Tabu List
        else
            TC(i)=max(TC(i)-1,0);   % Reduce Tabu Counter
        end
    end
    
    % Update Best Solution Ever Found
    if sol.Cost&lt;=BestSol.Cost
        BestSol=sol;
    end
    
    % Save Best Cost Ever Found
    BestCost(it)=BestSol.Cost;
    
    % Show Iteration Information
    disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);
    
    % Plot Best Solution
    figure(1);
    PlotSolution(BestSol, model);
    pause(0.01);
    
    % If Global Minimum is Reached
    if BestCost(it)==0
        break;
    end
    
end

BestCost=BestCost(1:it);

model = CreateModel();

CostFunction=@(tour) TourLength(tour, model);

ActionList=CreatePermActionList(model.n);

nAction=numel(ActionList);

%% Parameters

MaxIt=100;

TL=round(0.5*nAction);

%% Initialization

empty_individual.Position=[];

empty_individual.Cost=[];

% Create Initial Solution

sol=empty_individual;

sol.Position=randperm(model.n);

sol.Cost=CostFunction(sol.Position);

% Initialize Best Solution Ever Found

BestSol=sol;

% Array to Hold Best Costs

BestCost=zeros(MaxIt,1);

% Initialize Action Tabu Counters

TC=zeros(nAction,1);

%% Main Loop

for it=1:MaxIt

bestnewsol.Cost=inf;

% Apply Actions

for i=1:nAction

if TC(i)==0

newsol.Position=Action(sol.Position,ActionList{i});

newsol.Cost=CostFunction(newsol.Position);

newsol.ActionIndex=i;

if newsol.Cost<=bestnewsol.Cost

bestnewsol=newsol;

end

% Update Current Solution

sol=bestnewsol;

% Update Tabu List

for i=1:nAction

if i==bestnewsol.ActionIndex

TC(i)=TL; % Add To Tabu List

else

TC(i)=max(TC(i)-1,0); % Reduce Tabu Counter

end

% Update Best Solution Ever Found

if sol.Cost<=BestSol.Cost

BestSol=sol;

end

% Save Best Cost Ever Found

BestCost(it)=BestSol.Cost;

% Show Iteration Information

disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);

% Plot Best Solution

figure(1);

PlotSolution(BestSol, model);

pause(0.01);

% If Global Minimum is Reached

if BestCost(it)==0

break;

end

BestCost=BestCost(1:it);

برای دانلود مجموعه کامل و قابل اجرا در متلب الگوریتم جستجو ممنوع محصول را خریداری نمایید.

ویدئوی معرفی محصول

درباره محصول

سورس برنامه حل مسئله فروشنده دوره گرد TSP با الگوریتم جستجوی ممنوعه TS در متلب عنوان محصولی است که در این پست به آن پرداخته شده است. محصول در نرم افزار متلب نوشته شده و بصورت کامل توسط گروه پشتیبانی پی استور تست و اجرا شده است. محصول دارای نشان تضمین کیفیت پی استور می باشد. برای دانلود محصول آن را خریداری کنید. به محض خرید لینک دانلود در دسترس خواهد بود.

18,000 تومان

1 دیدگاه برای الگوریتم جستجوی ممنوعه TS برای حل مسئله فروشنده دوره گرد TSP در متلب

امتیاز 5 از 5
علیرضا سلطانی – ۱۳۹۸/۰۸/۰۶
ممنون از این کد متلب که آماده کردید. واقعاً بهترین جوابی که تا حالا گرفتم برای حل مسئله فروشنده دوره گرد یا همون TSP با الگوریتم جستجوی ممنوعه بوده اکثراً در تکرار کمتر از 50 جواب مسئله رو پیدا می کنه. من با الگوریتم های زیادی مسئله TSP رو آزمایش کردم (ژنتیک، PSO، الگوریتم مورچگان، زنبور، گرگ خاکستری، وال، پروانه، شمع و پروانه، فاخته، قورباغه، ملخ و …) ولی بهترین جواب برای حل مسئله TSP همین الگوریتم TS هست. فقط از ادمین محترم خواهشمندم فیلم آموزش کد نویسی رو هم در کنار کد متلب قرار بدن چون من خیلی زحمت کشیدم تا از کد سر در بیارم.
از دوستان عزیر که در مورد حل مسئله با الگوریتم های فرا اکتشافی کار می کنن خواهش دارم اگه نتایجی بهتر برای حل مسئله TSP دارن بفرمایند تا استفاده کنیم. ممنون از مدیریت محترم.
برای پاسخ وارد شوید
- programstore – ۱۳۹۸/۰۸/۰۶
  ممنون از اینکه نتایج خودتون رو مورد نقد و بررسی قرار دادید. ایشالا نظرات شما رو به برنامه نویسان و مدرسان مجموعه انعکاس می دیم.
  برای پاسخ وارد شوید

دیدگاه خود را بنویسید

این سایت از اکیسمت برای کاهش هرزنامه استفاده می کند. بیاموزید که چگونه اطلاعات دیدگاه های شما پردازش می‌شوند.

اطلاعات فروشنده

نام فروشگاه: پی استور
فروشنده: پی استور
آدرس: خیابان فردوس - بن بست فردوس 1 - پلاک 105
آذربایجان شرقی
5451358816
4.94 4.94 امتیاز از 237 دیدگاه

الگوریتم جستجوی ممنوعه TS برای حل مسئله فروشنده دوره گرد TSP در متلب

سورس کد الگوریتم جستجوی ممنوعه TS برای حل مسئله فروشنده دوره گرد TSP در متلب

الگوریتم جستجوی ممنوعه (Tabu Search) (TS)

حافظه recency :

حافظه frequency :

لیست ممنوع یا Tabu:

مسئله فروشنده دورگرد TSP

سور س حل مسئله فروشنده دوره گرد TSP با الگوریتم TS در متلب

ویدئوی معرفی محصول

درباره محصول

1 دیدگاه برای الگوریتم جستجوی ممنوعه TS برای حل مسئله فروشنده دوره گرد TSP در متلب

اطلاعات فروشنده

دیگر محصولات این فروشنده

تعیین درخت پوشای مینیمم با الگوریتم پریم در متلب

شبیه سازی الگوریتم TLBO در متلب

تبدیل دیتاست KDD99 برای استفاده الگوریتم های یادگیری ماشین در متلب

سورس کد الگوریتم زنبور عسل در متلب