الگوریتم کروسکال در Python برای حل مسئله درخت پوشای کمینه محصولی است که در این پست به آن پرداخته شده است. الگوریتم کروسکال یک روش حریصانه Heuristic در علوم کامپیوتر می باشد. از این الگوریتم برای حل مسئله درخت پوشا کمینه استفاده می شود. درخت پوشای کمینه یا همان مینیمم که به اصطلاح (MST (Minimum Spanning Tree نیز گفته می شود درختی است که در آن مجموع وزن لبه به حداقل برسد و تمامی گره ها یا راس ها شامل شود.

تهیه و تنظیم: تیم طراحی و تولید پی استور
متشکل از اساتید و فارغ التحصیلان رشته های فنی - مهندسی
تیم طراحی و تولید پی استور از اولین تیم های تشکیل شده در مجموعه آموزشی پی استور می باشد. این تیم از اساتید مجرب و فارغ التحصیلان رشته های فنی و مهندسی تشکیل شده که در زمینه های مختلف تولید محتوای تخصصی فعال هستند.
الگوریتم کروسکال Kruskal’s algorithm
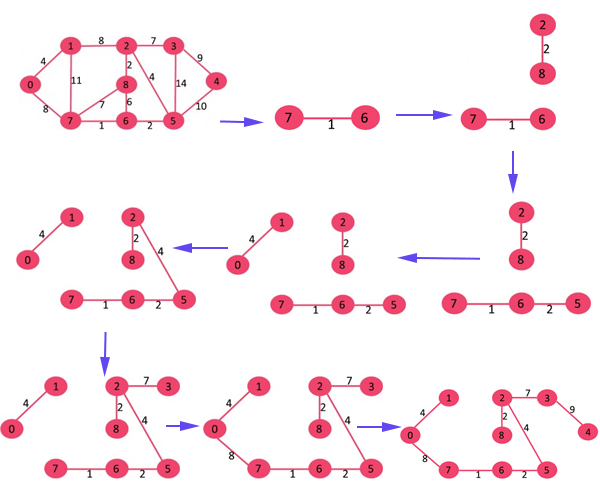
الگوریتم کروسکال برای پیدا کردن درخت پوشا بدین صورت عمل می کند ابتدا گراف G با n رأس را در نظر بگيريد.
1. تمام یال ها را به طور صعودی بر حسب وزن مرتب کنید.
2. درخت T را متشکل از گره های G بدون یال را ايجاد کنيد.
3. عملیات زیر را n-1 بارتکرار کنید:
4. یک یال با حداقل وزن را به درخت T اضافه کنید به طوری که حلقه ایجاد نشود.
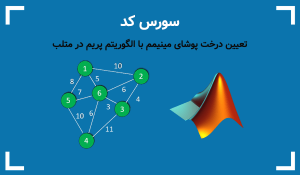
گاهی چند يال دارای يک وزن هستند، در اين حالت ترتيب يال هایی که انتخاب می شوند مهم نيست. درخت های پوشای حداقل مختلفی ممکن است حاصل شود اما مجموع وزن آنها هميشه يکسان و حداقل می شود. پيچيدگی زمانی الگوريتم (O(mn می شود. که m تعداد يال ها و n تعداد رئوس گراف G است. روند کلی الگوریتم برای یک مثال بصورت زیر است.
الگوریتم کروسکال در Python
پیاده سازی الگوریتم Kruskal’s در پایتون شامل توابعی است که مراحل بالا را انجام می دهد قسمتی از سورس کد الگوریتم کروسکال در Python به صورت زیر است.
from collections import defaultdict
#Class to represent a graph
class Graph:
def __init__(self,vertices):
self.V= vertices #No. of vertices
self.graph = [] # default dictionary
# to store graph
# function to add an edge to graph
def addEdge(self,u,v,w):
self.graph.append([u,v,w])
# A utility function to find set of an element i
# (uses path compression technique)
def find(self, parent, i):
if parent[i] == i:
return i
return self.find(parent, parent[i])
# A function that does union of two sets of x and y
# (uses union by rank)
def union(self, parent, rank, x, y):
xroot = self.find(parent, x)
yroot = self.find(parent, y)
# Attach smaller rank tree under root of
# high rank tree (Union by Rank)
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
# If ranks are same, then make one as root
# and increment its rank by one
else :
parent[yroot] = xroot
rank[xroot] += 1
.
.
.
g = Graph(4)
g.addEdge(0, 1, 10)
g.addEdge(0, 2, 6)
g.addEdge(0, 3, 5)
g.addEdge(1, 3, 15)
g.addEdge(2, 3, 4)
g.KruskalMST()
خروجی حاصل از اجرای الگوریتم نیز بصورت زیر خواهد بود.
Following are the edges in the constructed MST 2 -- 3 == 4 0 -- 3 == 5 0 -- 1 == 10
ویدئوی معرفی محصول
درباره سورس کد الگوریتم کروسکال
این محصول تحت عنوان سورس کد تعیین درخت پوشای مینیمم با الگوریتم کروسکال در Python در نوشته شده است. این برنامه مناسب برای دانشجویان و علاقه مندان به درس ساختمان داده و طراحی الگوریتم می باشد چرا که دارای کد های روان و قابل فهم و آسان برای یادگیری می باشد. خرید محصول توسط کلیه کارت های شتاب امکان پذیر است و بلافاصله پس از خرید، لینک دانلود محصول در اختیار شما قرار خواهد گرفت. کیفیت محصول توسط کارشناسان پی استور تضمین می شود.
مباحث مرتبط با الگوریتم کروسکال
مباحث پیشنهادی در حوزه حل درخت پوشای مینیمم
تعیین درخت پوشای مینیمم با الگوریتم کروسکال در Python
| تاریخ انتشار: | 29 اسفند 1397 |
|---|---|
| تاریخ بروزرسانی: | 14 شهریور 1398 |
| حجم فایل: | 1.3 کیلوبایت |
| فرمت فایل | py. در قالب پایتون |
| مدت زمان: | 1.0 |
| هماهنگی با: | (Spyder (Python 3.8 و بالاتر |
تاکنون 606 نفر این محصول را تهیه کرده اند و 2 نظر برای آن ثبت شده است.
نظرات و دیدگاه ها
قوانین ثبت دیدگاه
- لطفاً دیدگاه های خود را فارسی تایپ کنید.
- دیدگاه های نامرتبط به مطلب تایید نخواهد شد.
- از درج دیدگاه های تکراری پرهیز نمایید.
- سوالات تخصصی خودتان را از طریق تیکت پشتیبانی مطرح کنید.
تعیین درخت پوشای مینیمم با الگوریتم کروسکال در Python
هزینه سفارش: 99,000 تومان
| تاریخ انتشار: | 29 اسفند 1397 |
|---|---|
| تاریخ بروزرسانی: | 14 شهریور 1398 |
| حجم فایل: | 1.3 کیلوبایت |
| فرمت فایل | py. در قالب پایتون |
| مدت زمان: | 1.0 |
| هماهنگی با: | (Spyder (Python 3.8 و بالاتر |
2 بازخورد (مشاهده نظرات)
هزینه سفارش: 99,000 تومان





احمد
دمت گرم
احمد حیدری
من این محصول رو خریداری کردم ولی می خوام گراف خودم رو بهش بدم چیکار باید کنم؟
مدیریت و پشتیبانی
سلام
دوست عزیز برای وارد کردن گراف خودتان در سورس کد از ماتریس همسایگی گراف باید استفاده کنید.