الگوریتم بهینه سازی جستجوی گرانشی GSA

با پست الگوریتم بهینه سازی جستجوی گرانشی GSA مورد بررسی و واکاوی قرار خواهد گرفت. اگر برنامه نویس کامپیوتر هستید؛ به خوبی میدانید که امروزه محققان علوم کامپیوتر سعی دارند با الهام گرفتن از طبیعت و قوانین فیزیکی حاکم برا آن، الگوریتمهایی برای حل مسائل پیچیده Np-hard طراحی کنند. هرکدام از این الگوریتمهای بهینهسازی اغلب مبتنی بر جمعیتی یا مبتنی بر تصادف بوده؛ هرکدام برای هدف خاصی طراحی شده و اغلب اکتشافی هستند.
در الگوریتم بهینه سازی جستجوی گرانشی هم، همانطور که از نام آن پیداست از قانون جهانی گرانش نیوتن و برهمکنش اجسام برای طراحی و اجرای یک الگوریتم بهینهسازی فراابتکاری استفاده شده است. اصولا با پیدایش کلان داده و لزوم استفاده از سطح گستردهای از دادهها در انجام عملیات، تراکنشهای سیستمی و حل مسائل عموما پیچیده درهمتنیده، یک چالش بزرگ بهوجود آمد و آن هم این بود که در الگوریتمهای پیشنهادی باید در اسرع وقت و با صرف حداقل هزینه باید پاسخ بهینه خود را ارائه میکردند.
سالها پیش یک مهندس عمران، بهدفترم مراجعه کرده و درمورد مشکلش از بنده مشورت خواست. او و همکارش میخواستند سازههای خرپایی را که در بین سازندگان ساختمانی، بهدلیل سادهبودن و استحکام بالا معروف هستند؛ را با استفاده از الگوریتم بهینه سازی جستجوی گرانشی و با دو هدف کاهش وزن و افزایش استحکام سازه بهبود بخشند. آنها برای حل مشکلشان بهیک محقق علوم کامپیوتر نیاز داشتند تا در طراحی الگوریتم و ارائه راهکار بهینه کمکشان کند.
اگر شما هم مثل این دو مهندس جوان، با مشکل کمبود زمان و هزینه روبرو هستید و مشتاق شدهاید بدانید قانون جاذبه نیوتن چگونه در حل مسائل پیچیده حاکم بر علوم کامپیوتر و حتی چالشهای زندگی عادی، بهما کمک میکند تا انتهای این آموزش با ما همراه باشید.
نیروهای پایه طبیعت
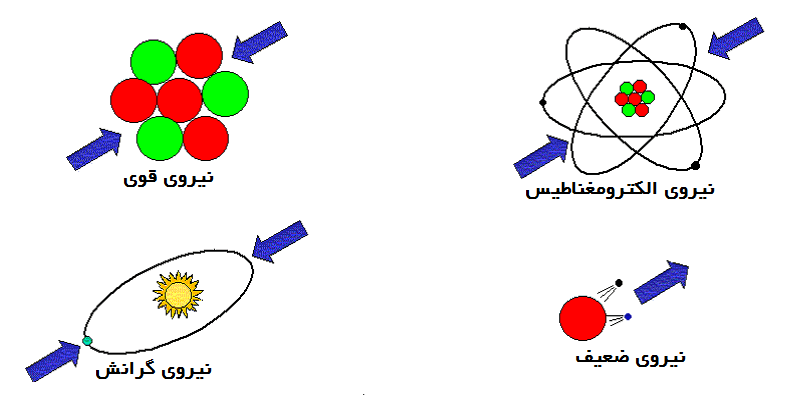
کاربران گرامی، قبل از شروع مبحث الگوریتم بهینه سازی جستجوی گرانشی GSA جالب است بدانید؛ در طبیعت چهار نوع نیرو وجود دارد کهبهعنوان نیروهای بنیادی شناخته میشوند و عبارتند از نیروی گرانش، نیروهای الکترومغناطیسی، نیروی هستهای ضعیف و کشش هستهای قوی. هر کدام از این نیروها دامنه و برد مربوط بهخود را دارد ولی اگر بخواهیم با دید مقایسهای نگاه کنیم؛ نیروی جاذبه نسبتبه هرکدام از آنها دارای قدرت کمتری میباشد ولی به خاطر داشتن محدوده وسعت زیاد نسبت بهدیگر نیروها فراگیر است؛ بهنحوی که تمام اجسام را با هدفی مشخص بههر سمتی که لازم باشد؛ میکشاند.
پاورپوینت آماده الگوریتم جستجوی گرانشی GSA
پاورپوینت آماده الگوریتم جستجوی گرانشی GSA در Microsoft Powerpoint در 24 اسلاید بصورت آکادمیک برای ارائه کلاسی طراحی و نگارش شده است. برای تهیه این پاورپوینت بر روی لینک زیر کلیک کنید.
در کتابهای درسی هم با قوانین نیوتن در کتاب فیزیک نهم آشنا میشوید و سپس در فیزیک دوازدهم با دید تحلیلی، دانستههایتان تکمیل میشود. میدانید که نظریهپردازان آیزاک نیوتن و آلبرت انیشتین که اولی فیلسوف طبیعت و دومی فیزیکدان است؛ بهکمک یکدیگر، تئوری جاذبه را در سطح کهکشانها و زمین بهجهانیان معرفی کردند.
این تئوری که پس از افتادن سیب از درخت بر روی سر نیوتن کلید خورد؛ درمورد بسیاری از عجایب خلفت ازجمله حرکت سیارهها، تولد سارگان و ساختار کهکشانها بحث کرده و رویای ساختن ماشین زمان را در ذهن بسیاری از محققان آفریده است. در ادامه، نیروهای بنیادی چهارگانه را ملاحظه میکنید.
اصول قانون جاذبه
قانون جاذبه نیوتن چند بخش دارد که دو بخش آن مربوط به مبحث الگوریتم بهینه سازی جستجوی گرانشی GSA میشود. نیوتن در بخش اول از تئوری جاذبه، بیان کردهاست که هر جسمی جسم دیگر را بهسمت خود جذب میکند ولی مقدار نیرویی که بهوسیله آن، هر جسمی انواع اجسام دیگر را به طرف خود میکشند؛ اولا با میزان جرم آنها، ثانیا با فاصلهشان از یکدیگر متناسب است. اگر در فرمولی که در ادامه آمده است G را ثابت گرانش در نظر بگیریم؛ میزان نیروی جاذبه بین دو جسم با استفاده از رابطه زیر محاسبه میشود.
در بخش دوم از تئوری جاذبه، قوانین مربوط بهحرکت اجسام مطرح شده است. بر طبق این قوانین، هر شئ همواره حالت سکون خود را حفظ کرده و در حالت پایدار خود باقی میماند یا حتی اگر درحال حرکت است؛ بهحرکت یکنواخت خود بر روی یک خط مستقیم ادامه میدهد. مگر اینکه تحت تاثیر یک یا چند نیرو، قرار گرفته و مجبور بهتغییر حالت شود. دقیقا مثل توپ بولینگ که به مسیر یکنواخت خود بر روی یک خط راست ادامه میدهد تا اینکه بهموانع برخورد کرده و تحت تاثیر نیروی این برخورد، از مسیر حرکتش منحرف شده و شتاب میگیرد. رابطه بین جرم اجسام، نیروی وارده و شتاب در این حالت، از رابطه زیر محاسبه میگردد.
از دو فرمول بالا میتوان نتیجه گرفت که هر جسمی، مشتاق است جسم دیگر را به سمت خود دعوت کند اما هرچه جسمی بزرگتر و نزدیکتر باشد؛ با نیرویی خارق العاده، دیگری را بهسمت خود میکشاند.
مسیریابی مبتنی بر الگوریتم جستجوی گرانشی GSA
داکیومنت مسیریابی مبتنی بر الگوریتم جستجوی گرانشی در شبکههای سیار موردی در 74 صفحه در قالب word و pdf بصورت زیپ شده قابل دانلود می باشد. برای تهیه این داکیومنت بر روی لینک زیر کلیک کنید.
قانون گرانش
دوستان عزیز، اجازه دهید قبل از شروع مبحث الگوریتم بهینه سازی جستجوی گرانشی، کمی هم به قانون گرانش بپردازیم. احتمالا برایتان جالب باشید که بدانید وقتی صحبت از جرم اجسام میشود؛ درواقع محققان با سهنوع جرم محاسبات خود را انجام میدهند که عبارتند از جرم اینترسی، جرم گرانشی فعال و جرم گرانشی منفعل. در ادامه بهتعریف هرکدام میپردازیم.
جرم اینرسی
در مبحث اینرسی یا لختی، از یک ویژگی در تمام اجسام صحبت میشود که برطبق این ویژگی، آن جسم دربرابر تغییر سرعت یا تغییر جهت حرکت مقاومت میکند. بهعبارت دیگر، برطبق این ویژگی، اجسام تمایل دارند؛ وضعیت سکون یا حالت قبلی خود را حفظ کنند. شما هم مثل من، با خواندن این تعریف یاد کودکان لجباز افتادید؟
جرم گرانشی فعال
میزان شدت نیروی گرانشی در اطراف یک جسم که درنهایت منجر به کنش میشود؛ با معیاری به نام جرم گرانشی فعال سنجیده میشود. هر چه جرم گرانشی فعال یک جسم بیشتر باشد؛ نيروی گرانشی بيشتری را در حول خود، تولید میکند.
جرم گرانشی منفعل
فیزیکدانان، قدرت اثر متقابل در میدان گرانشی که منجر بهعمل واکنش میشود را با معیاری به نام جرم گرانشی غیرفعال یا منفعل اندازه میگیرند. هر چه جرم گرانشی منفعل یک جسم بیشتر باشد؛ نيروی گرانشی بيشتری را تجربه میکند. از آنچه که گفته شد؛ نتیجه میگیریم که هر جسم تحت تاثير نيروی گرانشی ساير اجسام، تحت تاثیر شتابی قرار میگيرد که میزان آن شتاب با برآيند نيروهای وارد بر آن جسم و عکس جرم اينرسی آن متناسب است. به شکل زیر توجه کنید.
تعریف کلی الگوریتم بهینه سازی جستجوی گرانشی GSA
در الگوریتم بهینه سازی جستجوی گرانشی GSA با شبیهسازی قوانینی شبیه به قانون گرانش و قوانین حرکت نیوتن در یک سیستم فرضی از فضای جستوجو محلی و در بازههای زمانی گسسته یک الگوریتم بهینهسازی به حل مسئله میپردازد. حتما برایتان این سوال پیش آمده که در اینصورت جرم عاملها چگونه تعیین میشود؟ باید به اطلاعتان برسانم که جرم عاملها باتوجه به تابع هدف تعیین گردیده و بسته بهنوع هدف جرم گرانشی هر متغییر کم و زیاد میشود.
استراتژی موجود
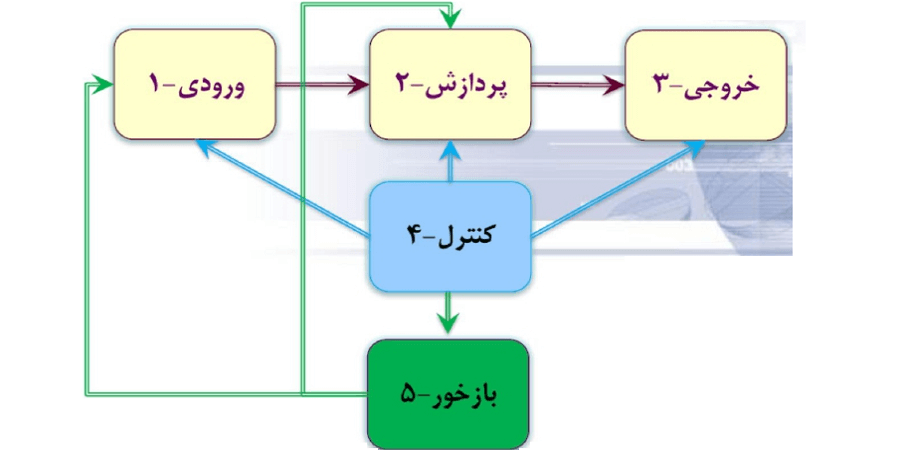
یک روند کلی در مورد استراتژی تمام الگوریتمها وجود دارد که طی یک نمودار آورده شده است.
درمورد الگوریتم بهینه سازی جستجوی گرانشی GSA، جهت جلوگیری از پیچیدگیهای احتمالی پیشنهاد میشود که قدم بهقدم پیش برویم. برای اینمنظور، چند گام اساسی وجود دارد که با طی کردن مرحله بهمرحله هرکدام از این گامها درنهایت یک نمونه کامل از الگوریتم بهینه سازی جستجوی گرانشی GSA خواهیم داشت که میتوانیم از آن برای حل مسائل پیچیده Np-hard استفاده کنیم.
فیلم آموزش حل فروشنده دوره گرد با الگوریتم GSA
در فیلم آموزش حل فروشنده دوره گرد یا همان TSP با الگوریتم GSA به توضیح خط به خط کد متلب مسئله فروشنده دوره گرد TSP با الگوریتم جستجوی گرانشی GSA پرداخته می شود. برای تهیه این آموزش بر روی لینک زیر کلیک کنید.
گام اول – تشکیل محیط یا سیستم فرضی
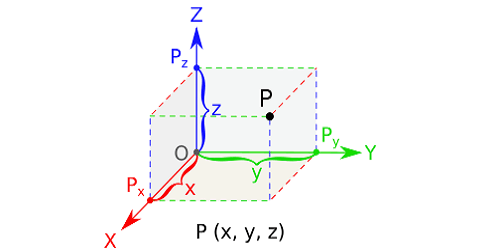
برای تعریف صورت مسئله، ابتدا یک دستگاه مختصات چندبعدی درنظر میگیریم. عاملهای جستجوگر مجموعهای از جرمهای فرضی را تشکیل داده و برای هرکدام از اجرام 4 مولفه موقعیت جرم، جرم اینرسی، جرم گرانشی فعال و جرم گرانشی منفعل درنظر میگیرند.
اجرام سهگانه قبلا توضیح داده شده است. اجرام گرانشی و برازندگی باتوجه بهتابع برازندگی هرکدام از عوامل مسئله تعیین میشوند. در مورد موقعیت جرم بهتر است که شفافسازی لازم صورت بگیرد. بهاین ترتیب که موقعیت جرم، بهعنوان نقطهای در فضا کهجواب مسئله است؛ درنظر گرفته میشود.
گام دوم – تعیین بازه زمانی گسسته در محیط جستوجوی محلی
بازه زمانی برای بررسی عملکرد الگوریتم بهینه سازی جستجوی گرانشی، گسسته است. به این دلیل که الگوریتم بتواند در هر لحظه از زمان که مدنظر کاربر باشد؛ عاملها را ارزیابی کند. شرط توقف الگوریتم میتواند پس از طی این بازه زمانی، یعنی پس از طی مدت زمان لازم برای بررسی در نظر گرفته شود.
گام سوم – موقعیتیابی تصادفی برای اجسام
با فرض اینکه فضای جستوجو در تمام ابعاد گسترده شدهباشد؛ قبل از شروع الگوریتم، عاملها بهصورت تصادفی موقعیتیابی میشوند. فضای بعدی میتواند چند بعدی باشد.
گام چهارم – تعریف دستورات مورد اجرا و قوانین کلی مسئله
اصلیترین قوانین الگوریتم بهینه سازی جستجوی گرانشی، قوانین حاکم برطبیعت گرانش و حرکت هستند که با اعمال تغییرات جزئی تعریف میشوند.
در قانون گرانش هر جرم تمام اجرام دیگر را با استفاده از نیرویی که برابر است با حاصلضرب جرم گرانشی فعال آن جرم در جرم گرانشی منفعل جرم دوم و عکس فاصله آن دو جرم؛ بهسمت خود جذب میکند. در قانون حرکت هم سرعت فعلی هر جرم برابر است با حاصل جمع ضريبی از سرعت قبلی جرم و میزان شتاب آن که برابر است با نيروی وارد بر آن تقسيم بر جرم اينرسی.
در الگوریتم بهینه سازی جستجوی گرانشی از نیروی جاذبه بهعنوان ابزار تبادل اطلاعات استفاده میشود. برطبق این الگوریتم، تمام عاملها متناسب با جرمشان، روی هم تاثير میگذارند و اثرگذاری آنها روی عمال نزدیکتر یا عامل همسایه بیشتر است.
گام پنجم – پیادهسازی الگوریتم GSA
در این مرحله، الگوریتم بهینه سازی جستجوی گرانشی GSA، شروع بهاجرای دستورات گرانش و حرکت میکند. سطر بهسطر دستورات نوشته شده توسط برنامهنویس را اجرا کرده و نتایج حاصل از اجرای الگوریتم را برمیگرداند. کاربران عزیز، بخشی از الگوریتم GSA در ادامه آورده شده است.
% Gravitational Search Algorithm.
function [Fbest,Lbest,BestChart,MeanChart]=GSA(F_index,N,max_it,ElitistCheck,min_flag,Rpower)
%V: Velocity.
%a: Acceleration.
%M: Mass. Ma=Mp=Mi=M;
%dim: Dimension of the test function.
%N: Number of agents.
%X: Position of agents. dim-by-N matrix.
%R: Distance between agents in search space.
%[low-up]: Allowable range for search space.
%Rnorm: Norm
%Rpower: Power of R
Rnorm=2;
%get allowable range and dimension of the test function.
[low,up,dim]=test_functions_range(F_index);
%random initialization for agents.
X=initialization(dim,N,up,low);
%create the best so far chart and average fitnesses chart.
BestChart=[];MeanChart=[];
V=zeros(N,dim);
for iteration=1:max_it
% iteration
%Checking allowable range.
X=space_bound(X,up,low);
%Evaluation of agents.
fitness=evaluateF(X,F_index);
if min_flag==1
[best best_X]=min(fitness); %minimization.
else
[best best_X]=max(fitness); %maximization.
end
if iteration==1
Fbest=best;Lbest=X(best_X,:);
end
if min_flag==1
if best<Fbest %minimization.
Fbest=best;Lbest=X(best_X,:);
end
else
if best>Fbest %maximization
Fbest=best;Lbest=X(best_X,:);
end
end
BestChart=[BestChart Fbest];
MeanChart=[MeanChart mean(fitness)];
%Calculation of M.
[M]=massCalculation(fitness,min_flag);
%Calculation of Gravitational constant.
G=Gconstant(iteration,max_it);
%Calculation of accelaration in gravitational field.
a=Gfield(M,X,G,Rnorm,Rpower,ElitistCheck,iteration,max_it);
%Agent movement.
[X,V]=move(X,a,V);
end %iteration
گام ششم – بررسی نتایج در گذر زمان و حرکت اجسام
در الگوريتم جستجوي گرانشی، مجموعهای از اجرام فضا را به صورت کاملا اتفاقی بررسی کرده و جستجو میکند. بنابراین، برنامه نویس باید الگوريتم را بهشکلی طراحی کند که در آن موقعيت جرمها با گذشت زمان بهبود پيدا کند. یافتهها حاکی از آن است که در نحوه حرکت هرکدام از عوامل، تاثیر عاملهاي با جرم سنگينتر بيشتر است. یعنی هرچه جرم سنگینتر باشد؛ شعاع تاثيرگذاری آن هم بهمراتب بزرگتر است.
بهبیان دیگر میتوان گفت که به اجرامی که تابع برازندگی مطلوبتری داشته باشند؛ جرم گرانشی بيشتری نسبت داده میشود. در نتيجه هر جرم به اندازه شايستگیش، ساير اجرام را به سمت خود جذب میکند. بنابراين، با گذشت زمان، اجرام به سمت موقعيتهای بهینهتری حرکت میکنند.
گام هفتم – بروز رسانی متغیرها
برای دست یافتن بهنتایج مطلوبتر، بهجرمهای بهتر، جرم اينرسی بزرگتری نسبت داده میشود. درنتیجه، هرعاملی که برازندگی بيشتری داشته باشد؛ فضای اطراف خود را با دقت بيشتری جستجو میکند. با گذشت زمان، جرمها دور موقعیتهای بهتر جمع شده و فضا را بهحالت فشرده درمیآورند. بنابراین، رفتهرفته ثابت گرانش کوچکتر شده و فضا با دقت بيشتری جستجو میشود. پس میتوان نتیجه گرفت که اين پارامتر، دقت جستجو را در تکرارهای مختلف الگوريتم کنترل میکند.
گام هشتم – بررسی شرط توقف الگوریتم و تکرار فرایند تا رسیدن به بهینه ترین حالت ممکن
الگوریتم در هر مرحله پس از یافتن موقعیت مناسب، بررسی میکند که آیا زمان اجرای الگوریتم بهپایان خود نزدیک شدهاست یا نه. شرط پایان الگوریتم باتوجه به پیچیدگی مسئله تعیین میشود. الگوریتم با بررسی آن شرط و تارسیدن به نتیجه مطلوب فرایند اجرای الگوریتم را تکرار میکند.
تشریح الگوریتم
دوستان و همراهان گرامی، خسته نباشید. بهقسمت جمعبندی گامهای الگوریتم رسیدهایم. اگر بخواهیم آنچه که بیان گردید را بهصورت خلاصه بیان کنیم؛ شبه کد زیر را خواهیم داشت.
کاربردهای الگوریتم GSA
عموما الگوریتمهایی که در آنها از قواعد طبیعی و بیولوژیکی بهره گرفته شده است؛ امروز مورد توجه کاربران و محققان علوم کامپیوتر قرار میگیرند و بسیار پرکاربرد هستند. الگوریتم بهینه سازی جستجوی گرانشی GSA هم در تمام علوم ازجمله علم پزشکی، علوم ساختمانی، فناوریهای دیجیتال، و علوم کامپیوتر بهکار گرفته میشود که مهمترین آنها عبارتند از: فرایند ترکیب تصاویر، تشخیص سرطان سینه، بهرهبرداری از سامانه برق آبی و چندمخزنه، مسیریابی در شبکههای سیار و سامانههای ماهوارهای، حل مسئله فروشنده دورهگرد، افزایش استحکام سازههای خرپایی، تشخیص بیماری عروق کرونری.
تشخیص سرطان سینه با الگوریتم جستجوی گرانشی و شبکههای عصبی مصنوعی
داکیومنت آماده تشخیص سرطان سینه با استفاده از الگوریتم جستجوی گرانشی و شبکههای عصبی مصنوعی در 72 صفحه در قالب ورد با نگارش آکادمیک و کامل ارائه گردیده است. برای تهیه این داکیومنت می توانید بر روی لینک زیر کلیک کنید.
کلام آخر در مورد الگوریتم بهینه سازی جستجوی گرانشی GSA
دوستان عزیز، الگوریتم بهینه سازی جستجوی گرانشی GSA یک الگوریتم فراابتکاری بسیار قدرتمند و بهینه در حوزه مسائل پیچیده تک مده و چند مده است. بهطوریکه میتواند با دیگر الگوریتمهای ابتکاری ترکیب شده؛ علی رغم نداشتن حافظه، سرعت اجرای بیشتری بهاجرای فرایند بخشیده و باعث بهبود عملکرد سیستم شود. برای تکمیل آموختههایتان و بررسی جامعتر این الگوریتم، میتوانید محصول سمینار الگوریتم جستجوی گرانشی GSA را از سایت دانلود کرده و مطالعه کنید.
درباره زهرا یاوری
کارشناس ارشد رشته علوم کامپیوتر از دانشگاه تبریز، مشاور و برنامهریز آزمونهای کارشناسی ارشد، پژوهشگر در حوزه علوم کامپیوتر، علاقمند به فعالیتهای تیمی، طراح صفحات وب، تحلیلگر سیستم، ایشان تحلیلگر ارشد شرکت بیمه البرز هستند و در زمینه علوم کامپیوتر سابقه تدریس دارند.


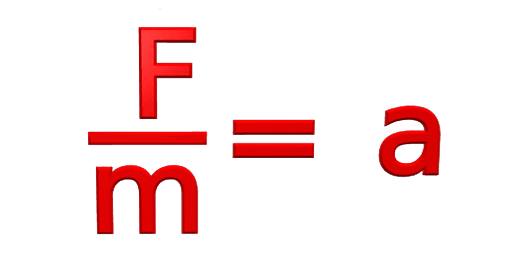












خیلی خوب و عالی بود.