تخفیف نوروزی پی استور
کد تخفیف: PR1404
شامل تمامی آثار
روز
ساعت
دقیقه
ثانیه
تخفیف نوروزی پی استور
یک درخت دودویی شرایط خاصی دارد که در آن هر گره در حالت ماگزیمم دو فرزند دارد. درخت جستجوی دودوی یک ساختار داده مبتنی بر گره است که دارای خواص زیر است:
عملیاتی که می‌توان در درخت دودویی انجام داد شامل جستجو Search، اضافه کردن یا درج Insertion و حذف Delete خواهد بود. که در ادامه این سه عملیات تشریح می‌شوند.
برای پیدا کردن گرهی با مقدار خاص در درخت، ابتدا باید از ریشه درخت شروع کنیم. اگر ریشه تهی باشد، درخت فاقد هر عنصری بوده و جستجو ناموفق خواهد بود. در غیر این صورت، key را با مقدار گره ریشه مقایسه می‌کنیم، اگر برابر بودند، جستجو موفق است و گره ریشه همان گره مورد نظر است. در غیر این صورت، دو حالت پیش خواهد آمد:
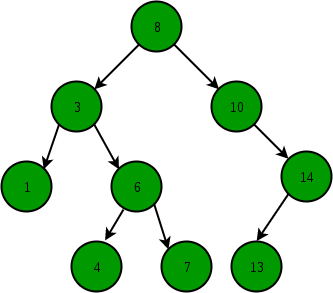
بسته به حالت ۱ و ۲، زیردرخت سمت چپ یا زیردرخت سمت راست را با استفاده از الگوریتم بالا جستجو می‌کنیم. عمل جستجو در درخت جستجوی دودویی، از مرتبه O(h) است که در آن h ارتفاع درخت است. چرا که حداکثر باید به میزان عمق درخت، به طرف پایین حرکت کنیم. برای مثال عدد ۶ را می‌خواهیم در درخت بالا جستجو کنیم. برای این کار عملیات زیر را باید انجام داد:
// C function to search a given key in a given BST
struct node* search(struct node* root, int key)
{
// Base Cases: root is null or key is present at root
if (root == NULL || root->key == key)
return root;
// Key is greater than root's key
if (root->key < key)
return search(root->right, key);
// Key is smaller than root's key
return search(root->left, key);
}
هر زمان که بخواهید یک عنصر در درخت اضافه یا درج کنید، ابتدا موقعیت مناسب را می‌یابید. جستجو از گره ریشه آغاز می‌شود، سپس اگر ارزش داده کمتر از ارزش کلید باشد، به دنبال موقعیت خالی در زیردرخت سمت چپ می‌گردیم و داده را در آن درج می‌کنیم. در غیر این صورت به دنبال یک موقعیت خالی در زیردرخت راست می‌گردیم و داده‌ها را درج می‌کنیم.
کد عملیات درج بصورت زیر خواهد بود.
struct node* insert(struct node* node, int key)
{
/* If the tree is empty, return a new node */
if (node == NULL) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
/* return the (unchanged) node pointer */
return node;
}
برای حذف یک عنصر از درخت دودویی ابتدا باید بررسی شود که عنصر مورد نظر در درخت وجود داشته باشد. اگر جواب مثبت باشد سه حالت پیش خواهد آمد.
حذف عنصر از برگ
این حالت ساده‌ترین حالت حذف می‌باشد. بدین صورت که عنصر پس از جستجو به‌راحتی از برگ حذف می‌شود شکل زیر نمونه‌ای از این عملیات است.
حذف عنصر با یک فرزند
گرهی که باید حذف شود اگر تنها یک فرزند داشته باشد. در این صورت عنصر حذف می‌شود و فرزند جایگزین گره حذف شده می‌شود. شکل زیر نمونه‌ای از این عملیات است.
حذف عنصر با دو فرزند
اگر گرهی که دو فرزند دارد حذف شود باید ابتدا گرهی با کوچک‌ترین مقدار در زیردرخت راست گره را پیدا می‌کنیم. درج این گره به جای گره قبلی شرایط درخت جستجوی دودویی را به هم نمی‌زند (چرا؟). در نتیجه می‌توان به راحتی آن را جایگزین کرد. شکل زیر نمونه‌ای از این عملیات است.
کد عملیات حذف بصورت زیر خواهد بود.
/* Given a binary search tree and a key, this function deletes the key
and returns the new root */
struct node* deleteNode(struct node* root, int key)
{
// base case
if (root == NULL) return root;
// If the key to be deleted is smaller than the root's key,
// then it lies in left subtree
if (key < root->key)
root->left = deleteNode(root->left, key);
// If the key to be deleted is greater than the root's key,
// then it lies in right subtree
else if (key > root->key)
root->right = deleteNode(root->right, key);
// if key is same as root's key, then This is the node
// to be deleted
else
{
// node with only one child or no child
if (root->left == NULL)
{
struct node *temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL)
{
struct node *temp = root->left;
free(root);
return temp;
}
// node with two children: Get the inorder successor (smallest
// in the right subtree)
struct node* temp = minValueNode(root->right);
// Copy the inorder successor's content to this node
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
return root;
}
در جستجو با استفاده از درخت جستجوی دودویی، در هر مرحله اگر به گره مورد نظر نرسیم، یک لایه در درخت به سمت پایین حرکت می‌کنیم. بنابراین تعداد مقایسه‌ها حداکثر برابر با عمق درخت است. حداقل تعداد مقایسه‌ها هم زمانی اتفاق می‌افتد که گره مورد نظر در رأس درخت قرار داشته باشد. در این حالت تنها یک مقایسه صورت می‌گیرد.
عمق یک درخت با n گره حداکثر n و حداقل log2n]+1] است. پس می‌توان گفت این روش جستجو حداقل از مرتبه‌ی یک، حداکثر از مرتبه‌ی n و به طور متوسط از مرتبه‌ی logn است. برای مطالعه بیشتر پیشنهاد می‌کنیم مقاله موجود در لینک زیر را مطالعه کنید.
نکته: در روش جستجوی دودویی در بدترین حالت هم مرتبه‌ی اجرا log n است. چرا که در هر مرحله به طور حتم داده‌ها به دو قسمت تقسیم می‌شوند. در نتیجه اگر یک درخت جستجوی دودویی و یک آرایه مرتب از مجموعه اعداد یکسان داشته باشیم، با صرفه‌تر است که از روش جستجوی دودویی برای جستجو استفاده کنیم. مگر آنکه درخت با توزیع مناسبی ساخته شده باشد و عمق آن حداقل باشد.
