Name: تعیین درخت پوشای مینیمم با الگوریتم پریم در پایتون Python
SKU: 5262
Price: 20000 IRT
Availability: InStock
Rating: 5.00 (1 reviews)

تعیین درخت پوشای مینیمم با الگوریتم پریم در پایتون Python

الگوریتم پریم در پایتون Python برای حل مسئله درخت پوشای کمینه عنوان محصولی است که در این پست به آن پرداخته شده است. الگوریتم پریم یک روش حریصانه Heuristic است. از این الگوریتم برای حل مسئله درخت پوشا مینیمم استفاده می شود. درخت پوشای کمینه یا همان مینیمم که به اصطلاح (MST (Minimum Spanning Tree نیز گفته می شود درختی است که در آن مجموع وزن لبه به حداقل برسد و تمامی گره ها یا راس ها شامل شود. در ادامه به توضیح کامل الگوریتم پریم در پایتون Python اشاره خواهد شد.

الگوریتم پریم PRIM’S ALGORITHM

الگوریتم پریم، الگوریتمی در نظریه گراف‌ها است که درخت پوشای مینیمم را برای یک گراف همبند وزن دار پیدا می‌کند. یعنی زیرمجموعه‌ای از یال‌ها را در آن گراف می‌یابد که درختی را تشکیل می‌دهند که همه راس ها را شامل شود و دارای حداقل هزینه یال ها باشد. این الگوریتم در سال ۱۹۵۷ توسط آقای پریم Prim، مطرح شد از این نوع دسته الگوریتم ها می توان به الگوریتم کروسکال و سولین نیز اشاره کرد.

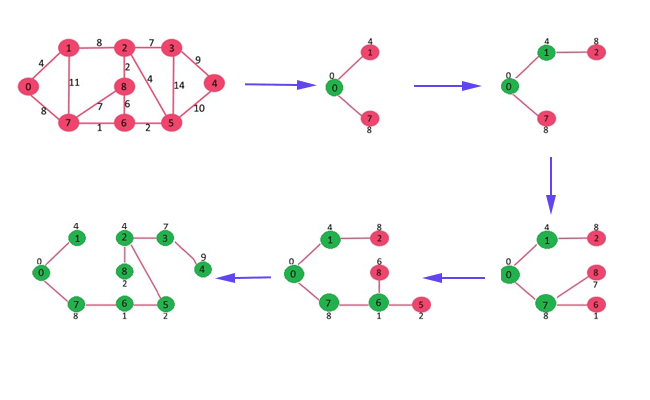
ایده اصلی الگوریتم پریم این است که دو مجموعه ای از رأس ها را نگه می دارد. مجموعه اول شامل رأس هایی است که قبلا در MST موجود است، مجموعه دیگری حاوی رأس هایی است که هنوز موجود نیستند. در هر مرحله همه لبه هایی که دو مجموعه را متصل می کنند را بررسی می کند و لبه ها با حداقل وزن انتخاب می شوند. پس از برداشتن لبه، نقطه انتهایی دیگر لبه را به مجموعه حاوی MST منتقل می کند. روند کلی الگوریتم برای یک مثال بصورت زیر است.

روند کلی الگوریتم پریم

الگوریتم پریم در پایتون Python

for cout in range(self.V): 
  
            # Pick the minimum distance vertex from  
            # the set of vertices not yet processed.  
            # u is always equal to src in first iteration 
            u = self.minKey(key, mstSet) 
  
            # Put the minimum distance vertex in  
            # the shortest path tree 
            mstSet[u] = True
  
            # Update dist value of the adjacent vertices  
            # of the picked vertex only if the current  
            # distance is greater than new distance and 
            # the vertex in not in the shotest path tree 
            for v in range(self.V): 
                # graph[u][v] is non zero only for adjacent vertices of m 
                # mstSet[v] is false for vertices not yet included in MST 
                # Update the key only if graph[u][v] is smaller than key[v] 
                if self.graph[u][v] > 0 and mstSet[v] == False and key[v] > self.graph[u][v]: 
                        key[v] = self.graph[u][v] 
                        parent[v] = u 
  
        self.printMST(parent) 
  
g = Graph(5) 
g.graph = [ [0, 2, 0, 6, 0], 
            [2, 0, 3, 8, 5], 
            [0, 3, 0, 0, 7], 
            [6, 8, 0, 0, 9], 
            [0, 5, 7, 9, 0]] 
  
g.primMST();

for cout in range(self.V):

# Pick the minimum distance vertex from

# the set of vertices not yet processed.

# u is always equal to src in first iteration

u = self.minKey(key, mstSet)

# Put the minimum distance vertex in

# the shortest path tree

mstSet[u] = True

# Update dist value of the adjacent vertices

# of the picked vertex only if the current

# distance is greater than new distance and

# the vertex in not in the shotest path tree

for v in range(self.V):

# graph[u][v] is non zero only for adjacent vertices of m

# mstSet[v] is false for vertices not yet included in MST

# Update the key only if graph[u][v] is smaller than key[v]

if self.graph[u][v] > 0 and mstSet[v] == False and key[v] > self.graph[u][v]:

key[v] = self.graph[u][v]

parent[v] = u

self.printMST(parent)

g = Graph(5)

g.graph = [ [0, 2, 0, 6, 0],

[2, 0, 3, 8, 5],

[0, 3, 0, 0, 7],

[6, 8, 0, 0, 9],

[0, 5, 7, 9, 0]]

g.primMST();

برای دریافت سورس کامل الگوریتم پریم در پایتون Python محصول را خریداری کنید.

ویدئوی معرفی محصول

درباره محصول

این محصول تحت عنوان سورس کد تعیین درخت پوشای کمینه با لگوریتم پریم در پایتون نوشته شده است. این برنامه مناسب برای دانشجویان و علاقه مندان به درس ساختمان داده و طراحی الگوریتم می باشد چرا که دارای کد های روان و قابل فهم و آسان برای یادگیری می باشد. خرید محصول توسط کلیه کارت های شتاب امکان پذیر است و بلافاصله پس از خرید، لینک دانلود محصول در اختیار شما قرار خواهد گرفت. کیفیت محصول توسط کارشناسان پی استور تضمین می شود.

programstore
28 اسفند 1397
امتیاز 5 از 5

پاسخ

نظرات و دیدگاه های خود را با ما درمیان بگذارید.

قوانین ثبت دیدگاه

دیدگاه های فینگلیش تایید نخواهند شد.
دیدگاه های نامرتبط به مطلب تایید نخواهد شد.
از درج دیدگاه های تکراری پرهیز نمایید.
امتیاز دادن به محصول فقط مخصوص خریداران آن می باشد.

لغو پاسخ

اطلاعات فروشنده

نام فروشگاه: پی استور
فروشنده: امین جلیل زاده رزین
آدرس: آذربایجان شرقی
4.93 4.93 امتیاز از 374 دیدگاه

پاورپوینت الگوریتم مرتب سازی موازی برای اتوماتای سلولی خطی

پی استور

30,000 تومان

پاورپوینت الگوریتم مرتب سازی موازی برای اتوماتای سلولی خطی با فرمت pptx. در 21 صفحه قابل دانلود است. بلافاصله پس از خرید، لینک دانلود محصول در دسترس خواهد بود.

با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:

دسترسی به فایل محصول به صورت مادام‌العمر
۶ ماه پشتیبانی کاملا رایگان و تضمین شده

خرید محصول

برنامه الگوریتم Best Fit در ++C سی پلاس پلاس

پی استور

18,000 تومان

این فایل در ویژوال ++C نوشته شده و بصورت زیپ شده قابل دانلود است. بلافاصله پس از خرید، لینک دانلود در اختیار شما قرار خواهد گرفت.

با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:

دسترسی به فایل محصول به صورت مادام‌العمر
۶ ماه پشتیبانی کاملا رایگان و تضمین شده

خرید محصول

الگوریتم‌های مسیریابی ترکیبی در شبکه‌های سیار موردی

پی استور

69,000 تومان

سمینار الگوریتم‌های مسیریابی ترکیبی در شبکه‌های سیار موردی در 47 صفحه در قالب word و pdf بصورت زیپ شده قابل دانلود است. به محض خرید محصول لینک دانلود در دسترس خواهد بود.

با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:

دسترسی به فایل محصول به صورت مادام‌العمر
۶ ماه پشتیبانی کاملا رایگان و تضمین شده

خرید محصول

تعیین درخت پوشای مینیمم با الگوریتم CMAES در متلب

پی استور

25,000 تومان

این فایل به زبان Matlab و بصورت zip شده قابل دانلود است. بلافاصله پس از خرید، لینک دانلود محصول در اختیار شما قرار خواهد گرفت.

با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:

دسترسی به فایل محصول به صورت مادام‌العمر
۶ ماه پشتیبانی کاملا رایگان و تضمین شده

خرید محصول

پروژه پردازش تصویر در سی شارپ #C

پی استور

22,000 تومان

این برنامه در ویژوال استادیو microsoft visual studio 2013 نوشته شده است و بلافاصله پس از خرید، لینک دانلود محصول در اختیار شما قرار خواهد گرفت.

با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:

دسترسی به فایل محصول به صورت مادام‌العمر
۶ ماه پشتیبانی کاملا رایگان و تضمین شده

خرید محصول

کد الگوریتم ژنتیک در پایتون Python

پی استور

25,000 تومان

این فایل به زبان پایتون و بصورت zip شده قابل دانلود است. بلافاصله پس از خرید، لینک دانلود محصول در اختیار شما قرار خواهد گرفت.

با خرید این محصول از مزایای زیر بهره‌مند می‌شوید:

دسترسی به فایل محصول به صورت مادام‌العمر
۶ ماه پشتیبانی کاملا رایگان و تضمین شده

خرید محصول

تعیین درخت پوشای مینیمم با الگوریتم پریم در پایتون Python